Fundamentos del ANOVA

Author
Affiliation

Mtro. Santiago Ríos

Cursos Orca

Introducción al Análisis de Varianza (ANOVA)

El Análisis de Varianza (ANOVA, por sus siglas en inglés) es una técnica estadística utilizada para comparar las medias de tres o más grupos o muestras. Fue desarrollado por Ronald A. Fisher en la década de 1920. La prueba de ANOVA permite determinar si existen diferencias estadísticamente significativas entre las medias de diferentes grupos, basándose en la variabilidad dentro de los grupos y entre los grupos. Sin embargo, ANOVA no indica cuáles grupos son diferentes entre sí; para ello, se utilizan pruebas post-hoc.

En esta lección, vamos a ver los fundamentos del ANOVA, incluyendo los conceptos clave, los supuestos, los tipos de ANOVA y cómo realizar un ANOVA paso a paso en R. Además, veremos cómo interpretar los resultados y cómo verificar los supuestos del ANOVA. En las próximas lecciones, veremos cómo realizar ANOVA en R de forma sencilla y cómo visualizar los resultados con ggpubr de manera directa.

¿Por qué utilizamos ANOVA para probar hipótesis?

Cuando queremos comparar las medias de más de dos grupos, hacer múltiples pruebas t individuales aumenta el riesgo de cometer errores de Tipo I (falsos positivos). ANOVA ofrece una solución al proporcionar una prueba estadística única que evalúa si hay al menos una diferencia significativa entre las medias de los grupos, controlando adecuadamente la tasa de error de Tipo I.

Conceptos clave en ANOVA

  • La varianza es una medida de dispersión que indica cuánto varían los datos respecto a la media. En ANOVA, la varianza se utiliza para comparar la variabilidad dentro de los grupos y entre los grupos.

En la figura observamos que cada grupo tiene distintas medias y varianza. Además, hay grupos con medias más cercanas y otros, como el 1, con medias más alejadas de los otros grupos.

Suma de cuadrados Entre-grupos y dentro de los grupos

  • La suma de cuadrados representa una medida de variación o desviación con respecto a la media. Se calcula como una suma de los cuadrados de las diferencias con respecto a la media.
  • Se calcula elevando al cuadrado la diferencia entre cada punto de datos y la media de los datos, y luego sumando todas las diferencias al cuadrado.
  • La Suma de Cuadrados se puede dividir en dos partes: la Suma de Cuadrados dentro de grupos y la Suma de Cuadrados entre grupos.
    • Suma de cuadrados entre grupos (SSB o SSTr): Mide la variabilidad de las medias de cada grupo respecto a la media general. es una medida de la variabilidad dentro de cada grupo. La suma de cuadrados dentro de grupos también se conoce como suma de cuadrados de error.
    • Suma de cuadrados dentro de los grupos (SSW o SSE): Mide la variabilidad de las observaciones dentro de cada grupo respecto a las medias de sus respectivos grupos. Es una medida de la variabilidad entre los grupos. La Suma de Cuadrados entre grupos también se conoce como suma de cuadrados de tratamiento.

Relación o razón F

  • La razón F es el estadístico utilizado en ANOVA para comparar la variabilidad entre los grupos con la variabilidad dentro de los grupos.
  • La razón F es la relación entre las medias cuadráticas entre los grupos y las medias cuadráticas dentro de los grupos.
  • Se utiliza para probar la hipótesis nula en ANOVA.

\[ F = \frac{SSB / df_{entre}}{SSE / df_{dentro}} \]

Donde:

  • SSB: Suma de cuadrados entre grupos.
  • SSE: Suma de cuadrados dentro de los grupos.
  • df: Grados de libertad.

La lógica de ANOVA

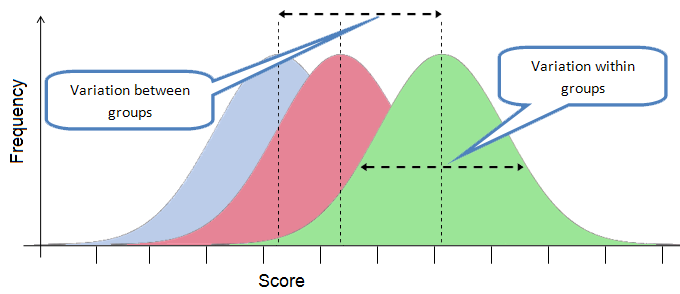
ANOVA se basa en comparar dos estimaciones de la varianza poblacional:

  1. Varianza entre grupos: Estima la varianza poblacional a partir de la variabilidad entre las medias de los grupos.
  2. Varianza dentro de los grupos: Estima la varianza poblacional a partir de la variabilidad dentro de cada grupo.

Si todas las medias son iguales, esperamos que estas dos estimaciones de la varianza sean aproximadamente iguales.

Si al menos una media es diferente, la varianza entre grupos será mayor que la varianza dentro de los grupos.

En este ejemplo, hay poca variación dentro de los grupos, pero mucha entre los grupos. En este caso, el valor F será alto. Esto se debe a que el numerador de la fórmula de F (variación entre los grupos) es grande, y el denominador (variación dentro de los grupos) es pequeño. Entonces, el valor p será bajo y probablemente, significativo. Esto indica que las diferencias entre los grupos son estadísticamente significativas.

En este ejemplo, hay más variación dentro de los grupos, pero poca entre los grupos. Valor F: Será bajo. La variación dentro de los grupos (denominador) es grande en comparación con la variación entre los grupos (numerador).Valor p: Será alto (probablemente no significativo). Esto indica que las diferencias observadas entre las medias de los grupos no son estadísticamente significativas.
  • Si \(F\) es aproximadamente igual a 1: Indica que la variabilidad entre grupos es similar a la variabilidad dentro de los grupos; no hay evidencia para rechazar la hipótesis nula.
  • Si \(F\) es significativamente mayor que 1: Sugiere que la variabilidad entre grupos es mayor de lo esperado bajo la hipótesis nula; hay evidencia para rechazar H₀.

El valor de \(F\) se compara con un valor crítico de la distribución F para obtener un valor p correspondiente.

Hipótesis en ANOVA

Hipótesis nula H_0

Todas las medias poblacionales son iguales:

\[ H_0: \mu_1 = \mu_2 = \dots = \mu_k \]

Hipótesis alternativa H_a

Al menos una de las medias poblacionales es diferente:

\[ H_a: \text{Al menos una } \mu_i \text{ es diferente} \]

Tipos de ANOVA

Veamos algunos tipos comunes de ANOVA. Cada tipo se utiliza en diferentes situaciones y con diferentes diseños experimentales. Además, cada tipo de ANOVA tiene sus propios supuestos y consideraciones. Veremos en las siguientes lecciones que en R podemos hacer cualquier tipo de ANOVA de forma sencilla.

ANOVA de una vía (One-way ANOVA)

  • Compara las medias de tres o más grupos independientes basados en un solo factor o variable independiente.
  • Ejemplo: Comparar el rendimiento académico entre estudiantes de tres métodos de enseñanza diferentes.

ANOVA de dos vías (Two-way ANOVA)

  • Compara las medias considerando dos factores o variables independientes, y puede evaluar el efecto de cada factor y su interacción.
  • Ejemplo: Evaluar el efecto del método de enseñanza y el género en el rendimiento académico.
  • Este análisis no solo permite probar los efectos individuales de cada factor (efectos principales), sino también la interacción entre los factores.
  • Una interacción ocurre cuando el efecto de un factor depende del nivel del otro factor. Por ejemplo, en un estudio sobre el crecimiento de plantas, puede haber una interacción entre el tipo de suelo y el nivel de fertilizante. Si la interacción es significativa, la interpretación de los efectos principales se vuelve más compleja, ya que el efecto de un factor no es constante a través de los niveles del otro.

ANOVA de medidas repetidas (Repeated Measures ANOVA)

  • Utilizado cuando las mismas unidades experimentales son medidas bajo diferentes condiciones o tiempos.
  • Ejemplo: Comparar el rendimiento de los estudiantes de 3 grupos al inicio, a mitad y al final del semestre.

Supuestos de ANOVA

Para que los resultados del ANOVA sean válidos, se deben cumplir ciertos supuestos:

  1. Independencia de las observaciones:
    • Las observaciones son independientes entre los grupos y dentro de los grupos.
    • Asegurado mediante un diseño adecuado y aleatorización.
  2. Normalidad:
    • Las distribuciones de los residuos (diferencias entre las observaciones y las medias de los grupos) son aproximadamente normales.
    • Puede verificarse mediante pruebas de normalidad y gráficos (histogramas, Q-Q plots).
  3. Homogeneidad de varianzas (homocedasticidad):
    • Las varianzas dentro de los grupos son aproximadamente iguales.
    • Puede evaluarse con pruebas como la de Levene o de Bartlett.

Si estos supuestos no se cumplen, se pueden considerar transformaciones de datos o utilizar pruebas no paramétricas alternativas, como el test de Kruskal-Wallis.

Ejemplo, paso por paso

Vamos a ver un ejemplo en R utilizando tidyverse que ejemplifica cada uno de los pasos del ANOVA. Utilizaremos un conjunto de datos simulado para representar las diferentes dietas y la presión arterial sistólica de los participantes. Al final, verás que todos estos pasos se pueden realizar de forma sencilla con la función aov() en R. Además, en las siguientes lecciones, veremos cómo hacer todos estos pasos y graficar los resultados con ggpubr.

Visualización inicial de los datos

Es útil visualizar los datos para tener una comprensión inicial.

Plantear las hipótesis

  • Hipótesis nula \(H_0\): Las medias de la presión arterial sistólica son iguales para todas las dietas.
  • Hipótesis alternativa \(H_a\): Al menos una de las medias de la presión arterial sistólica es diferente.

Calcular las sumas de cuadrados

Calcular la media general

Calcular las medias por grupo

Suma total de cuadrados (SST)

\[ \text{SST} = \sum_{i=1}^{N} (Y_i - \bar{Y})^2 \]

Suma de cuadrados entre grupos (SSB)

\[ \text{SSB} = \sum_{j=1}^{k} n_j (\bar{Y}_j - \bar{Y})^2 \]

Suma de cuadrados dentro de los grupos (SSW)

\[ \text{SSW} = \sum_{j=1}^{k} \sum_{i=1}^{n_j} (Y_{ij} - \bar{Y}_j)^2 \]

Verificación:

\[ \text{SST} = \text{SSB} + \text{SSW} \]

Calcular los grados de libertad

Calcular las medias cuadráticas Media cuadrática entre grupos (MSB):

\[ \text{MSB} = \frac{\text{SSB}}{df_{\text{entre}}} \]

Media cuadrática dentro de los grupos (MSW):

\[ \text{MSW} = \frac{\text{SSW}}{df_{\text{dentro}}} \]

dentro ​ ::: {.cell autorun=‘true’}

:::

Calcular el estadístico F

\[ F = \frac{\text{MSB}}{\text{MSW}} \]

Determinar el valor p o comparar con el valor crítico

Calculamos el valor p asociado al estadístico F calculado.

Decisión:

  • Nivel de significancia \(\alpha = 0.05\)
  • Si \(\text{valor p} < \alpha\) , rechazamos \(H_0\)​

Verificación con la función aov()

Para confirmar nuestros cálculos, utilizamos la función aov().

Observamos que los valores de Sum Sq, Mean Sq, F value y Pr(>F) coinciden con nuestros cálculos manuales.

Conclusión: Hay diferencias significativas en la presión arterial sistólica promedio entre las dietas.

Pruebas Post-hoc

Como encontramos diferencias significativas, podemos realizar pruebas post-hoc para identificar entre qué dietas existen diferencias.

Cuando ANOVA indica diferencias significativas, pero no especifica qué grupos difieren entre sí. Las pruebas post-hoc se utilizan para realizar comparaciones pares controlando el error de Tipo I.

  • Prueba de Tukey HSD
  • Prueba de Bonferroni
  • Prueba de Scheffé

Usaremos la prueba de Tukey HSD para controlar el error de Tipo I.

  • Después de realizar las pruebas post-hoc, podemos identificar específicamente entre qué dietas hay diferencias significativas en la presión arterial sistólica.
  • Observa qué grupos tienen diferencias significativas y cuáles no. El valor de la p adj indica el valor p ajustado para controlar el error de Tipo I. Si este valor es menor que \(\alpha\), se considera significativo.
    • La primera columna indica la comporación entre grupos.

Visualización de los resultados Post-hoc

Verificación de supuestos

Normalidad de los residuos - podemos usar la prueba de Shapiro-Wilk y el gráfico Q-Q para verificar la normalidad de los residuos. - La prueba de Shapiro-Wilk evalúa si los residuos siguen una distribución normal. La hipótesis nula es que los residuos son normales.

Si el valor p es mayor que 0.05, no rechazamos la normalidad de los residuos.

Gráfico Q-Q:

Homogeneidad de varianzas

Usamos la prueba de Levene.

  • La hipótesis nula es que las varianzas son iguales entre los grupos.

Si el valor p es mayor que 0.05, no rechazamos la igualdad de varianzas.

Resumen final

  • Hipótesis nula rechazamos H_0: Hay diferencias significativas entre las dietas.

  • Pruebas post-hoc: Identifican específicamente entre qué dietas hay diferencias.

  • Supuestos del ANOVA: Fueron verificados y cumplidos.

Resumen

  • ¿Qué es ANOVA? Una técnica estadística para comparar las medias de tres o más grupos.
  • ¿Cómo funciona? Compara la variabilidad entre grupos con la variabilidad dentro de los grupos usando el estadístico F.
  • ¿Por qué se usa para probar hipótesis? Permite evaluar si hay diferencias significativas entre las medias de los grupos, controlando el error de Tipo I sin realizar múltiples pruebas t.
  • Supuestos clave: Independencia, normalidad y homogeneidad de varianzas.
  • Tipos de ANOVA: Una vía, dos vías, factorial, medidas repetidas.
  • Cuando se rechaza \(H_0\): Indica que al menos una media es diferente y se deben utilizar pruebas post-hoc para identificar las diferencias específicas.