Prueba t y el Test de Rango de Wilcoxon

Author

Affiliation

Mtro. Santiago Ríos

Introducción

La prueba t de una muestra y el test de rango de Wilcoxon son herramientas fundamentales para evaluar si la media de una muestra es significativamente diferente de un valor hipotético. Ambos tests pueden interpretarse como modelos lineales simples, donde el objetivo es predecir la media de la variable dependiente.

Prueba t de muestra única: Evalúa si la media de una muestra es significativamente diferente de un valor de referencia.
Test de rango con signo de Wilcoxon: Es una alternativa no paramétrica a la prueba t para muestras únicas, que evalúa si la mediana de una muestra es significativamente diferente de un valor de referencia, utilizando los rangos de los datos en lugar de los valores originales.

Puntos Clave

Prueba t de muestra única como modelo lineal: El modelo lineal en este caso predice la media de la variable dependiente (\(y\)):

\[ y = \beta_0 \]

donde \(\beta_0\) es la media de la muestra y se compara con el valor de referencia (hipótesis nula: \(\beta_0 = 0\).

Note

Observa que la ecuación anterior es lo mismo que:

\[ y = \beta_0 + \beta_1 \cdot x \]

Solamente que no ponemos el último término ya que no tenemos una variable independiente (recuerda que estamos hablando de una muestra única). Por lo tanto, \(x = 0\).

Test de Wilcoxon como modelo lineal: Similar a la prueba t, pero en lugar de usar los valores originales de \(y\), se utilizan los rangos con signo de \(y\):

\[ {rango.signo}(y) = \beta_0 \]

Este test es útil cuando los datos no cumplen con los supuestos de normalidad.

rango con signo

Previamente, vimos que si ordenamos en rango con la función rank(c(3.6, 3.4, -5.0, 8.2)), el resultado es 3, 2, 1, 4.
Un rango con signo es lo musmo, pero el rango se obtiene, primero con el tamaño absoluto y luego se le asigna el signo original. En el ejemplo anterior, el rango con signo sería 2, 1, -3, 4.

Equivalencia de los tests con modelos lineales: Tanto la prueba t como el test de Wilcoxon pueden expresarse como un modelo lineal simple, lo que permite interpretar los resultados de manera similar.

Ejemplo en R: Prueba t de una muestra y Test de Wilcoxon

A continuación, vamos a realizar ambos tests (t-test y Wilcoxon) utilizando R y visualizaremos los resultados.

Paso 1: Generar los datos

Vamos a trabajar con los datos guardados en la variable D_t1, que contiene una muestra de 20 observaciones con una media de 0.5 y una desviación estándar de 0.6.

Paso 2: Visualización

El siguiente gráfico muestra los datos y la media de la muestra y (0.5) en azul. Los datos individuales están etiquetados con su valor.

Ahora, aplicamos la transformación de rangos con signo a los mismos datos y creamos una gráfica similar. No te preocupes si no entiendes el código, lo importante es que veas la gráfica y los rangos.

t-test

La prueba t de una muestra puede realizarse fácilmente con la función t.test() en R, pero también se puede obtener el mismo resultado usando un modelo lineal con la función lm(). - Observa que para el modelo lineal, usamos y ~ 1 para indicar que solo estamos interesados en la media de la variable y, es decir, el intercepto. - En la función t.test(), especificamos la variable y del dataset D_t1. - Vamos a obtener los mismos resultados con ambos métodos: - La prueba t de una muestra: - media = 0.5 - valor-p = 0.00143 - Modelo lineal: - coeficiente = 0.5 - p-valor = 0.00143

Test de Rango con Signo de Wilcoxon

El test de Wilcoxon se puede realizar con la función wilcox.test(), y también se puede realizar usando un modelo lineal aplicado a los rangos con signo. - Sin embargo, en este caso, los resultados no serán exactamente iguales, ya que el test de Wilcoxon y el modelo lineal tienen diferentes distribuciones de referencia para calcular el valor p. - En ambos casos se rechabza la hipótesis nula de que la media es cero, pero los valores p son diferentes. Abajo del gráfico se explica por qué.

Important

En el test de Wilcoxon, el estadístico es la suma de los rangos con signo (estadístico V).
En el modelo lineal, el estadístico es el valor t asociado al intercepto del modelo, que estima la media de los rangos con signo.
Aunque ambos enfoques están relacionados con los rangos con signo, el test de Wilcoxon y el modelo lineal tienen diferentes distribuciones de referencia para calcular el valor p (veremos esto en el tema siguiente de prueba de hipótesis).
- El test de Wilcoxon utiliza la distribución exacta de los rangos
- El modelo lineal utiliza la distribución t

Regresaremos a la discusión de cómo diferentes pruebas pueden producir valores p diferentes en el tema de prueba de hipótesis. Por ahora soloobserva que podemos realizar la prueba de Wilcoxon con un modelo lineal o con la función wilcox.test().

Pruebas t para Muestras Pareadas y Test de Wilcoxon

muestra pareada: se refiere a dos mediciones tomadas en la misma unidad experimental, como antes y después de un tratamiento, o dos mediciones en el mismo individuo.

Teoría: Pruebas t para Muestras Pareadas

En una prueba t para muestras pareadas, el objetivo es evaluar si las diferencias entre dos mediciones (por ejemplo, antes y después de un tratamiento) son significativamente diferentes de cero. Esto se puede interpretar como un modelo lineal donde la diferencia entre las dos mediciones es el valor de \(y\):

\[ y_2 - y_1 = \beta_0 \]

La hipótesis nula \(H_0\) en este caso es \(\beta_0 = 0\).

De manera similar, el test de Wilcoxon para pares es la versión no paramétrica de la prueba t para muestras pareadas y se basa en los rangos con signo de las diferencias entre las dos muestras:

\[ {rango.signo}(y_2 - y_1) = \beta_0 \]

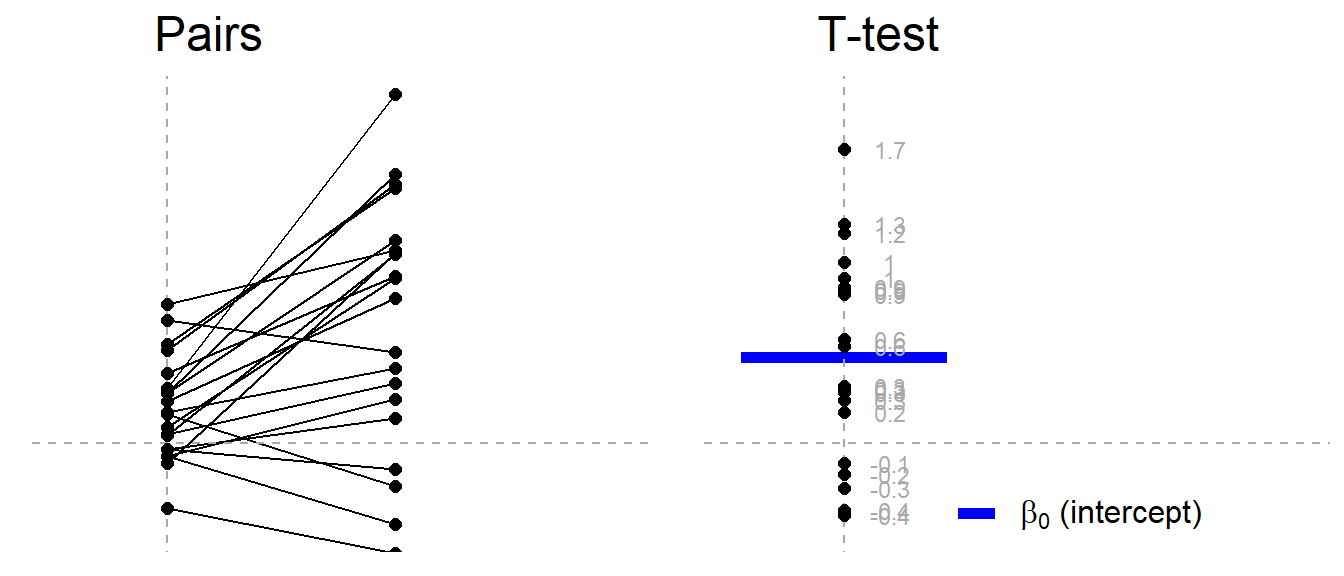
Simplificando un poco, puedes pensar que la diferencia de medias en este caso son pendientes, como en la figura izquierda que presenta los datos de un mismo individuo en un tiempo 1 y un tiempo 2. Estas diferencias de pendientes se pueden evaluar mediante la prueba t-pareada, como en la figura de la derecha.

Códigos en R: Prueba t para Muestras Pareadas

Vamos a trabajar con los datos guardados en los vectores antes y despues, que contiene dos mediciones (antes y después) de 10 sujetos.

Para la prueba t para muestras pareadas, usamos la función t.test() con el argumento paired = TRUE.

Para hacerlo como un modelo lineal, tenemos que usar la notación: lm(y - y2 ~ 1)

Note

Ves que obtenemos los mismos resultados con ambos métodos?
- En la prueba t para muestras pareadas:
  - media de las diferencias = -0.54
  - valor-p = 0.0492
- En el modelo lineal:
  - coeficiente (intercepto) = -0.54
  - p = 0.0492

Códigos en R: Test de Wilcoxon para Pares

El test de Wilcoxon para pares es la versión no paramétrica de la prueba t para muestras pareadas y se basa en los rangos con signo de las diferencias entre las dos muestras. - De nuevo, los valores p serán similares, pero no exactamente iguales.

Las pruebas NO paramétricas NO comparan medias!!

Como hemos visto y observaras en el output anterior, las pruebas no paramétricas no comparan las medias como lo hacen las pruebas paramétricas. En su lugar, estas pruebas se basan en rangos en lugar de valores absolutos.

En las pruebas paramétricas (como el t-test o ANOVA), se comparan las medias entre los grupos o condiciones.
En las pruebas no paramétricas, no se comparan directamente las medias. En lugar de ello, se comparan medianas, rangos o distribuciones de los datos. Esto hace que las pruebas no paramétricas sean más robustas cuando los datos no son normales o contienen valores atípicos.

Conclusión

Las pruebas t de muestra única y para muestras pareadas, junto con sus contrapartes no paramétricas (Wilcoxon), son herramientas poderosas para evaluar diferencias en medias. Al entender que estos tests pueden expresarse como modelos lineales simples, podemos unificar el análisis de estas pruebas y aplicar este conocimiento a una amplia variedad de datos y situaciones.

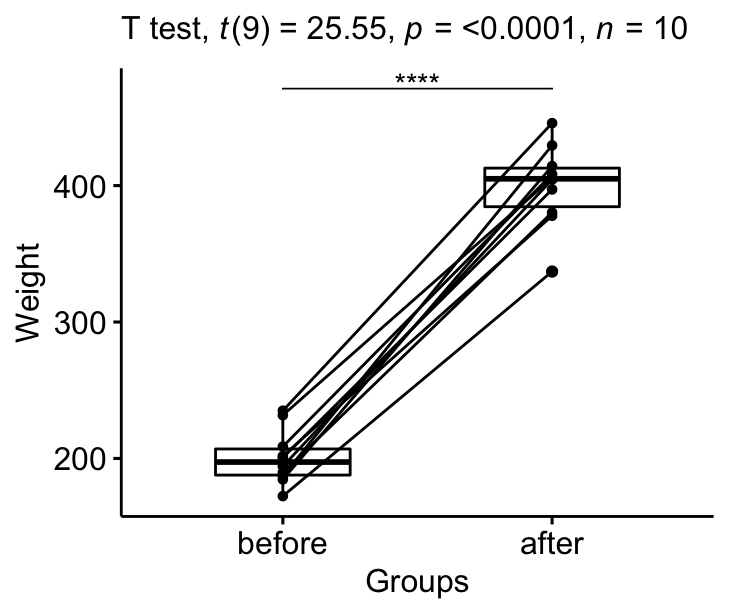
Más adelante, veremos cómo usar ggpubr para visualizar los resultados de estas pruebas y obtener gráficos con los resultados de los tests: