Supuestos de los Modelos Lineales

Author

Affiliation

Mtro. Santiago Ríos

Un supuesto en estadística es una condición que debe cumplirse para que un modelo o método sea válido. Para que un modelo lineal funcione correctamente se deben cumplir estos supuestos:

Linealidad

La relación entre el predictor \(x\) y la variable respuesta \(y\) es lineal. Es decir, el cambio en \(y\) debido a un cambio en \(x\) es constante.

Linealidad NO es lo mismo que recta

Linealidad en el contexto de los modelos lineales no significa necesariamente que la relación entre las variables deba formar una línea recta en el gráfico. En lugar de referirse a la forma de la gráfica, la linealidad en los modelos lineales se refiere a cómo los parámetros (o coeficientes) del modelo se combinan con las variables predictoras. Por ejemplo, consider la siguiente ecuación de un modelo lineal:

\[ y = \beta_0 + \beta_1 \cdot x^4 \]

Aunque la relación entre \(x\) y \(y\) no es una línea recta, el modelo sigue siendo lineal porque los coeficientes \(\beta_0\) y \(\beta_1\) se combinan de manera lineal con \(x\).

¿Cómo se vería una relación NO lineal? Si los coeficientes están involucrados en operaciones no lineales (exponenciales o elevados al cuadrado), perderíamos la linealidad del modelo. Por ejemplo:

\[ y = e^{\beta_0 + \beta_1 \cdot x} \]

Residuos

Los residuos de un modelo lineal deben cumplir ciertos supuestos. Antes de verlos, vamos a definir qué son los residuos en un modelo lineal.

Los residuos en un modelo lineal son las diferencias entre los valores observados (p. ej. los que obtenemos en nuestro experimento) y los valores predichos por el modelo.
Estos residuos son una medida de cuánto se desvían los datos reales de la línea de regresión ajustada.
Los residuos son una parte clave del modelo, ya que representan el error o la incertidumbre que no puede ser explicada por las variables predictoras. Un buen modelo de regresión tendrá residuos pequeños y distribuidos de manera aleatoria alrededor de la línea de regresión.
Vamos a ver esto con ejemplos para que quede más claro.

Ejemplo

Vamos a ver cómo se ven los residuos en un modelo lineal.
Primero, vamos a ajustar un modelo de regresión lineal simple con datos simulados.
En el siguiente gráfico, la línea roja representa la regresión lineal, los puntos naranjas son los datos observados (p.ej. los datos que obtuvimos en un experimento).
Las líneas negras representan los residuos. Observa que los residuos son las distancias verticales entre los puntos observados y la línea de regresión.

Click para ver el código usado en el gráfico

Regresemos al ejemplo de la relación entre la masa corporal y el largo de la aleta de los pingüinos.
Vamos a ajustar un modelo de regresión lineal y visualizar los residuos de todos los datos.
La línea roja representa la regresión lineal, los puntos naranjas son los datos observados y las líneas negras representan los residuos.

Click para ver el código usado en el gráfico

Important

¿Cómo se ajusta la recta de regresión a los datos?
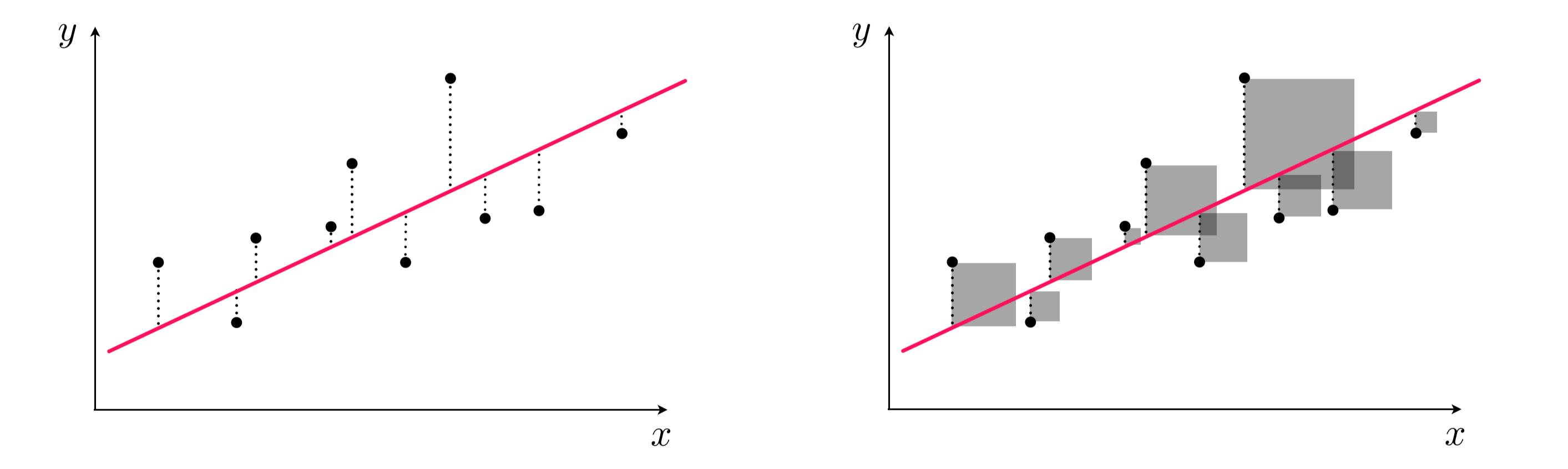
- La recta de regresión se ajusta minimizando la suma de los cuadrados de los residuos. Es decir, la recta se ajusta de tal manera que la suma de las distancias verticales entre los puntos observados y la recta es la menor posible.
- Esto se conoce como el método de los mínimos cuadrados.
- Observa la siguiente figura para entender cómo se ajusta la recta de regresión a los datos:

La ssuma de cuadrados trata de minimizzar el área total de los cuadrados grises que se observan en la derecha

Supuesto de residuos

Normalidad

Los residuos (diferencias entre los valores observados y los predichos por el modelo) deben seguir una distribución normal. Esto significa que los residuos deben estar distribuidos simétricamente alrededor de cero y seguir una forma de campana similar a la distribución normal, como en el siguiente gráfico:

Homocedasticidad

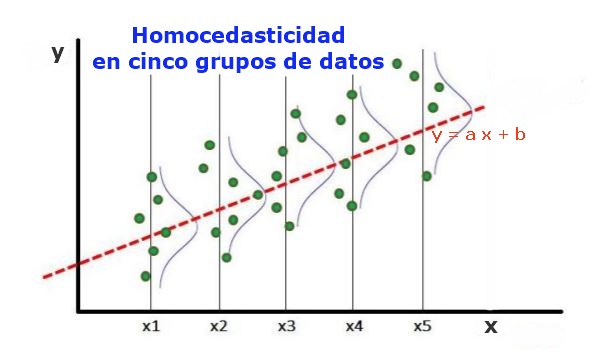
La homocedadasticidad es la propiedad de los residuos de un modelo lineal de tener una varianza constante a lo largo de todos los niveles de los predictores. En otras palabras, la dispersión de los residuos debe ser constante en todos los valores de las variables predictoras. Lo contrario es llamado heterocedasticidad.

La varianza de los residuos es constante para todos los valores de las variables predictoras. En otras palabras, el ruido en las predicciones del modelo debe ser el mismo a lo largo de todos los niveles de los predictores.

Heterocedasticidad. En valores bajos de X, hay poca varianza de los residuos, mientras que en valores altos, hay mucha más varianza. Esto se obsreva como un cono.

Verificación de los supuestos de los residuos

Para verificar la normalidad de los residuos, se pueden utilizar pruebas estadísticas como la prueba de Shapiro-Wilk o gráficos como el gráfico Q-Q o gráficos de residuos.
Vamos a ver los gráficos primero.

Primero, tenemos que ajustar el modelo lineal. Vamos a hacerlo con los datos de los pingüinos. En la lección pasada vimos la función lm() para ajustar un modelo lineal. Vamos a hacerlo de nuevo. Esta función tomará como argumentos la fórmula del modelo y los datos donde se encuentran las variables de la siguiente manera: lm(y ~ x, data = datos). En este caso, la variable respuesta es el largo de la aleta (largo_aleta_mm) y la variable predictora es la masa corporal (masa_corporal_g). Ajusta el modelo y guarda el resultado en una variable llamada modelo_pinguinos. Los datos pinguinos_clean ya están cargados y limpios (sin valores faltantes).

gráfico de residuos

Ahora, para hacer el gráfico de residuos con ggplot, vamos a hacer un gráfico de dispersión con los valores ajustados de la variable predictora en el eje x (los valores predichos por el modelo = .fitted) y los residuos en el eje y (las diferencias entre los valores observados = .resid). El dataframe es el modelo que ajustamos en la celda anterior.
En el valor de cero en el eje x, los residuos deberían estar distribuidos aleatoriamente alrededor de la línea horizontal en 0. Esto indicaría que los residuos siguen una distribución normal y que el supuesto de normalidad se cumple.

Cómo nos ayuda este gráfico a verificar los supuestos de los residuos?

Si los residuos siguen una distribución normal, esperaríamos que los puntos estén distribuidos aleatoriamente alred y alrededor de la línea horizontal en 0.
Si hay patrones en la distribución de los residuos (p.ej. forma de embudo, curvas, etc.), esto podría indicar que los residuos no siguen una distribución normal y que el supuesto de normalidad no se cumple.
Si la varianza de los residuos cambia a lo largo de los valores ajustados, esto podría indicar que el supuesto de homocedasticidad no se cumple.
En el gráfico anterior, ¿qué observas sobre la normalidad y homocedasticidad de los residuos?

Observa ejemplos de gráficos de residuos donde se cumplen y no se cumplen los supuestos de normalidad y homocedasticidad:

Linearidad es válida porque la media de los residuos está cercana a 0 y la dispersión de los residuos es similar

Linearidad es válida, pero la varianza no es constante: en valores altos de valores predichos, hay mucha más dispersión. La figura de cono que observamos es

El supuesto de linearidad no parece cumplirse porque la media de los residuos no está cercana a cero

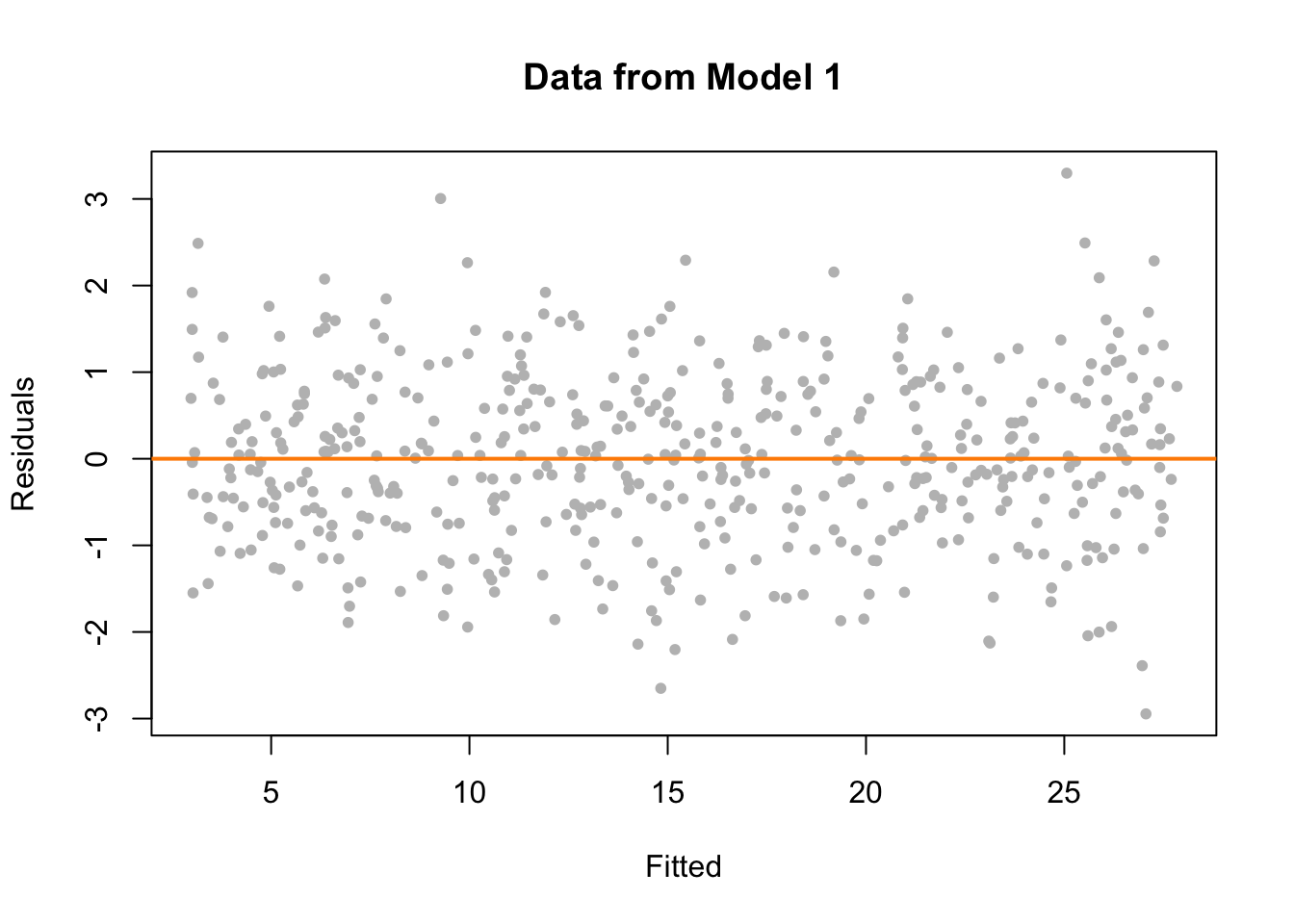
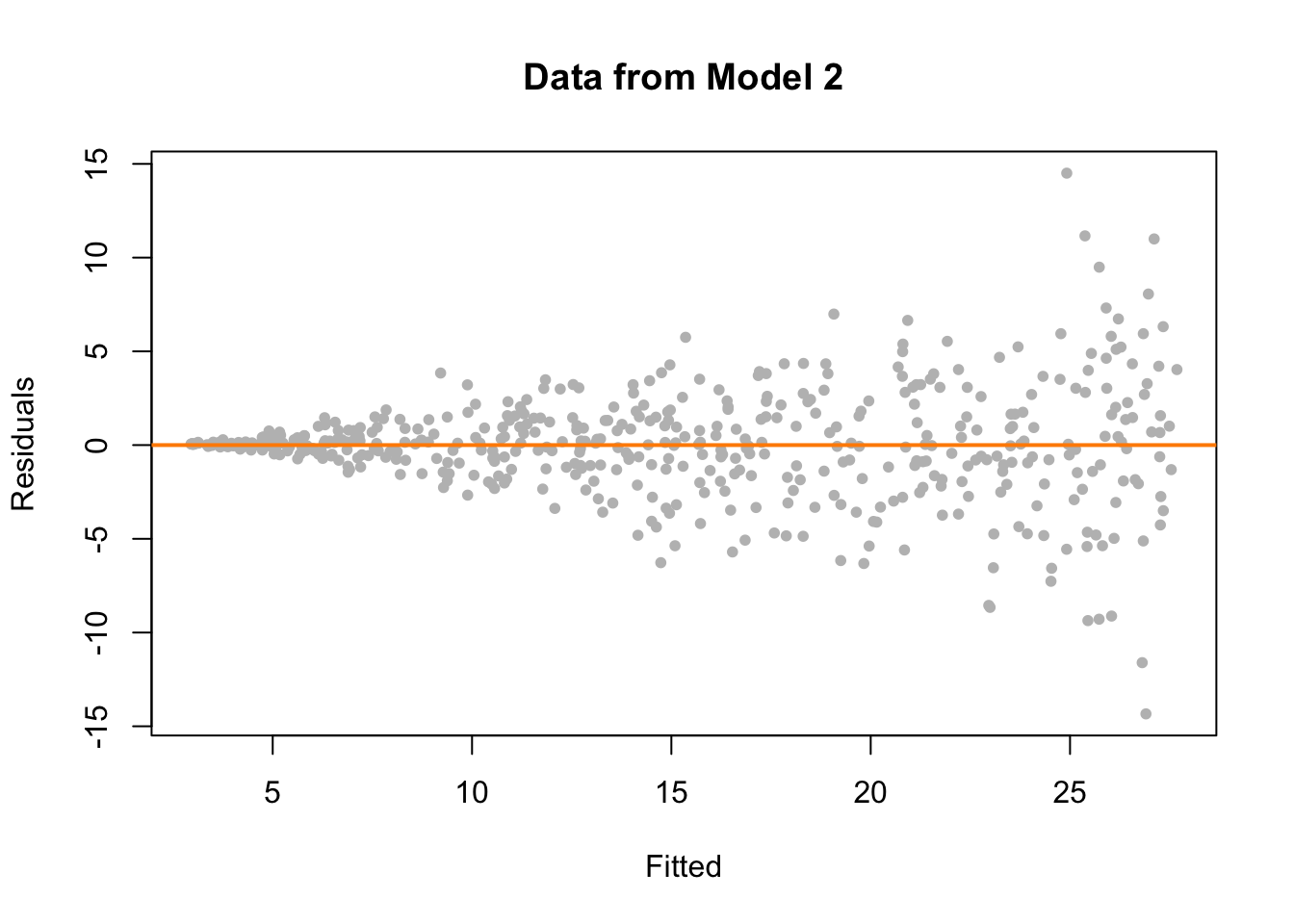
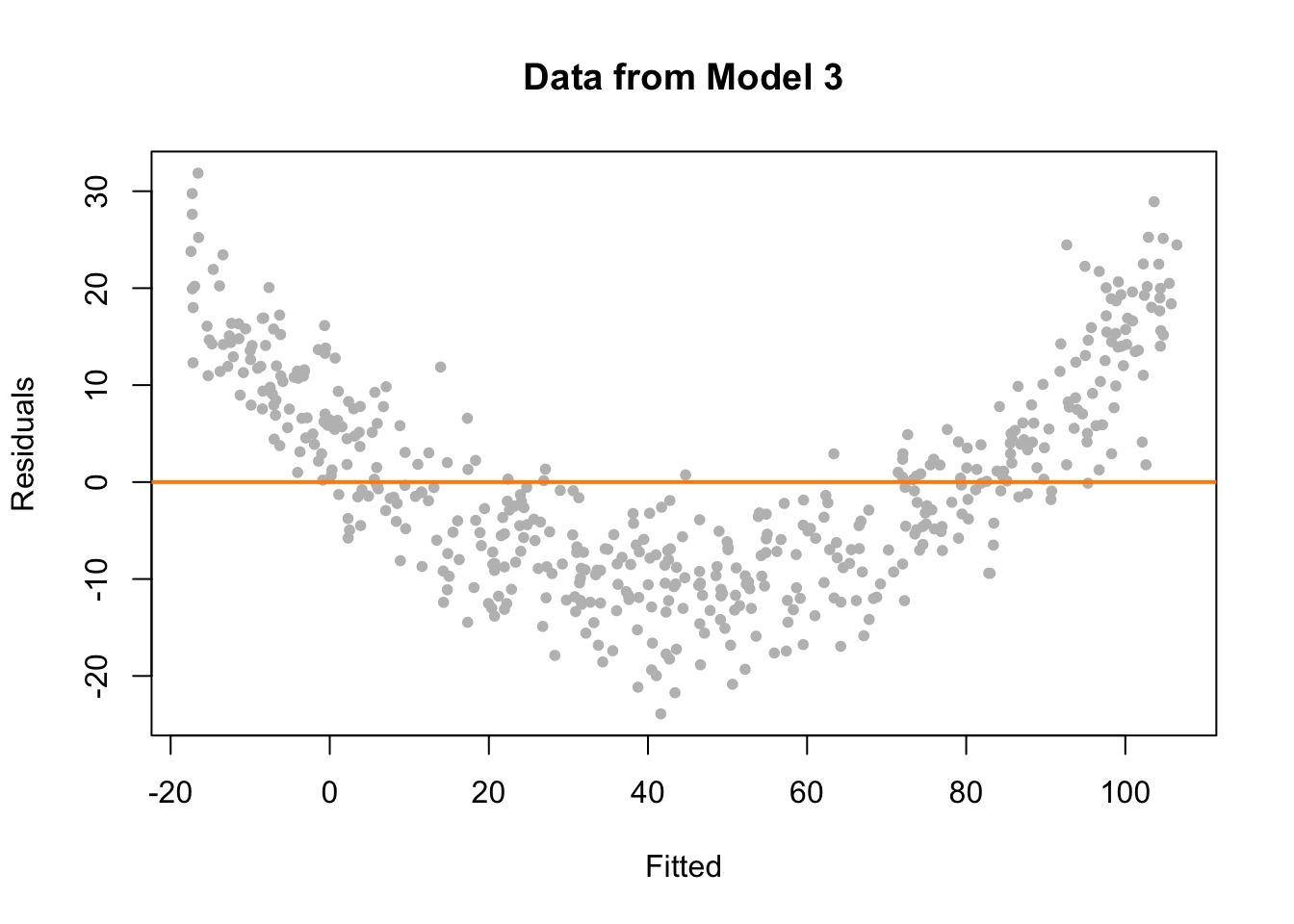
gráfico Q-Q

Otra forma de verificar la normalidad de los residuos es mediante un gráfico Q-Q (cuantil-cuantil). Este gráfico compara los cuantiles de los residuos con los cuantiles de una distribución normal. Si los residuos siguen una distribución normal, los puntos en el gráfico Q-Q deberían seguir una línea diagonal.
En las siguientes figuras, el gráfico Q-Q de la izquierda muestra una distribución normal de los residuos, mientras que el de la derecha muestra una distribución no normal.

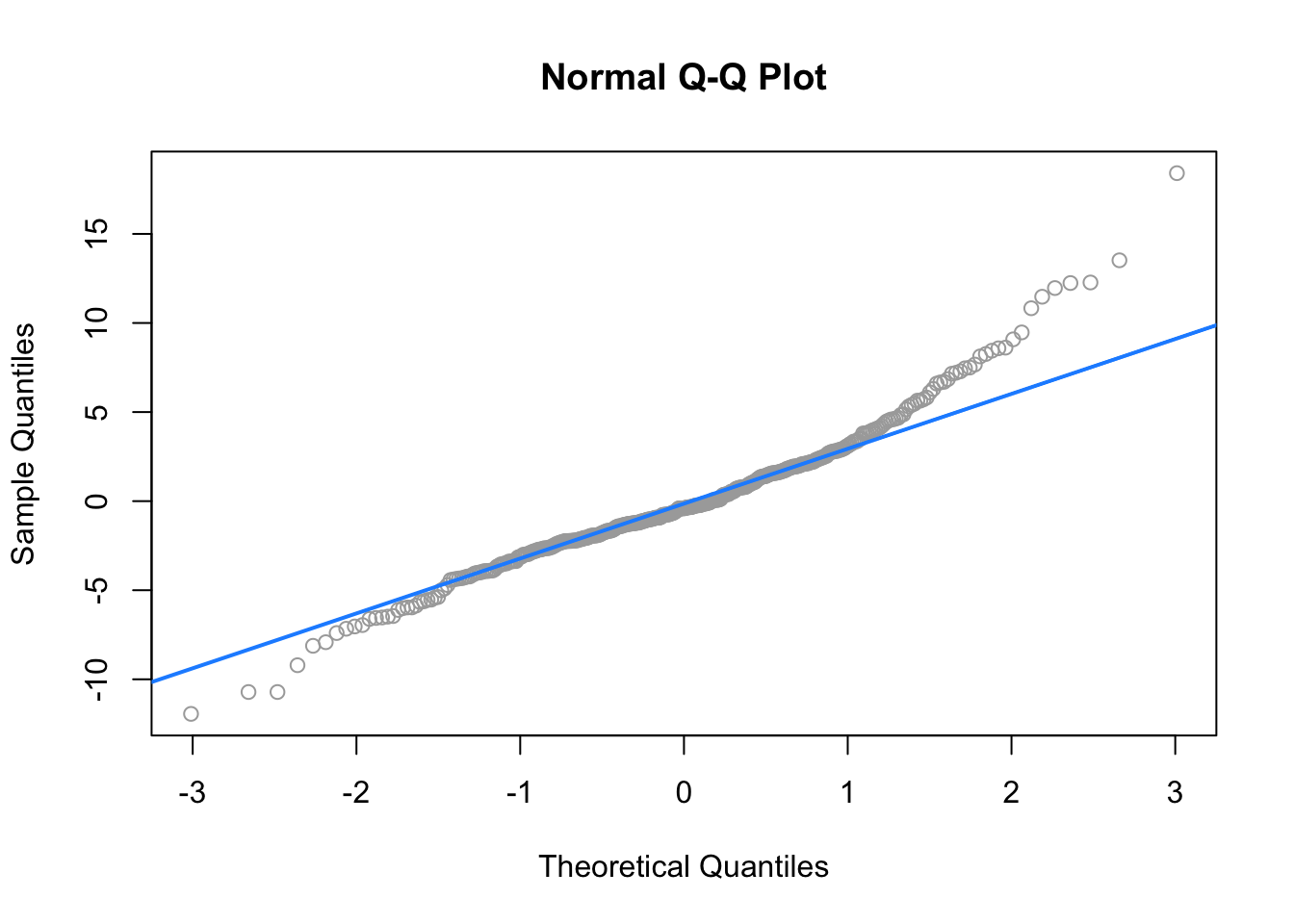
Ahora, para hacer el gráfico Q-Q de los residuos del modelo de los pingüinos, vamos a usar la función stat_qq() y stat_qq_line de ggplot.

Reflexión

¿Son o no son normales los residuos del modelo de regresión lineal de los pingüinos?
Regresaremos a esta discusión al final de este tema.
Podemos contestar esta pregunta con una prueba estadística, como la prueba de Shapiro-Wilk, que evalúa si los residuos siguen una distribución normal, pero esto se verá después de que veamos qué son las pruebas de hipótesis.
Cuando los supuestos no se cumplen, el modelo puede proporcionar predicciones sesgadas o intervalos de confianza incorrectos, los cuales también veremos más adelante.
Sin embargo, existen técnicas para manejar o ajustar estos problemas, como transformaciones de los datos o el uso de modelos más robustos.

Evaluación del Modelo

Veremos esto en detalle en futuras lecciones, pero es importante mencionar que una vez que hemos ajustado un modelo lineal, es necesario evaluar su desempeño. Algunas de las métricas más comunes incluyen:

\(R^2\) : También conocido como el coeficiente de determinación, mide la proporción de la variabilidad en \(y\) que es explicada por el modelo. Un valor de \(R^2\) cercano a 1 indica que el modelo explica bien los datos, mientras que un valor cercano a 0 sugiere que el modelo no captura mucha de la variabilidad en la variable respuesta.
Pruebas de hipótesis: Se utilizan para evaluar la significancia de los coeficientes del modelo. Un p-valor bajo para un coeficiente \(\beta_i\) sugiere que la variable \(x\) tiene un impacto significativo sobre \(y\).
Análisis de residuos: Verificar si los residuos siguen una distribución normal y si su varianza es constante puede ayudar a diagnosticar problemas con el ajuste del modelo.