Introducción a Modelos Lineales en Estadística

Author

Affiliation

Mtro. Santiago Ríos

Introducción a los Modelos Lineales

La mayoría de las pruebas estadísticas comunes utilizadas en ciencias de la salud y biológicas, como el t-test, ANOVA, correlación, y otras, son casos especiales de modelos lineales o aproximaciones muy cercanas a ellos. Esta simplicidad subyacente nos permite simplificar el proceso de aprendizaje y enseñanza de la estadística. En lugar de tratar cada prueba estadística como una herramienta aislada, podemos enfocar el aprendizaje en el modelo lineal general y luego reconocer cada prueba como una variación de este modelo.

Puntos clave del módulo:

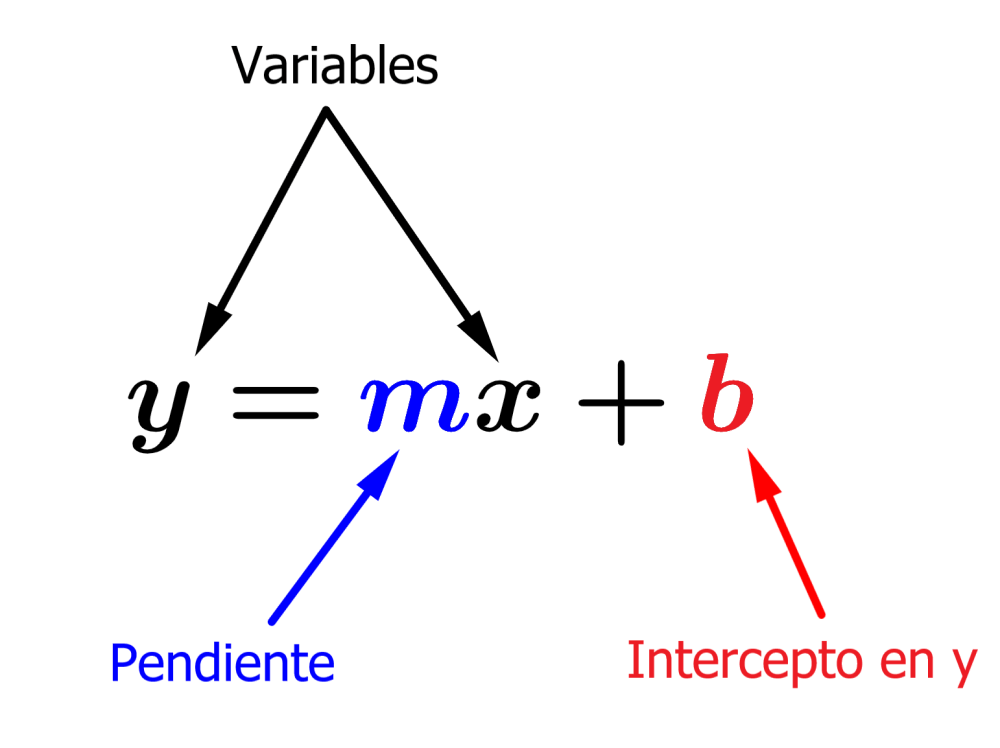
Simplicidad del modelo lineal: Un modelo lineal sigue la fórmula básica: \[ y = a \cdot x + b \]

donde \(y\) es la variable dependiente, \(x\) es la variable independiente, \(a\) es la pendiente de la recta, y \(b\) es la intersección con el eje \(y\). Esta simplicidad subyacente es la base de muchas pruebas estadísticas comunes.

Evitar la memorización: En lugar de memorizar las suposiciones paramétricas de cada prueba estadística por separado, los estudiantes pueden deducirlas a partir del modelo lineal, lo que simplifica el aprendizaje. Muchas veces es dificil recordar los supuestos de cada prueba, ¿qué tipo de distribución tienen los datos?, ¿son independientes?, ¿son homocedásticos?, etc. En su lugar, podemos recordar que el modelo lineal tiene supuestos más generales y que las pruebas específicas son casos especiales de este modelo.

Enseñar modelos lineales primero: Al enseñar primero los modelos lineales y luego introducir los casos especiales (como el t-test o ANOVA), se promueve una comprensión más profunda de la estadística, en lugar de simplemente aprender mecánicamente cómo aplicar cada prueba.

Pruebas no paramétricas: Las pruebas “no paramétricas” pueden enseñarse como versiones ordenadas (ranking) de las pruebas paramétricas correspondientes. De esta forma, los estudiantes entienden que estas pruebas se basan en rangos y no en supuestos mágicos de eliminación de restricciones. Entenderás esto más adelante.

Aplicaciones en ciencias de la salud y biológicas: En estas disciplinas, el uso de modelos lineales es fundamental para analizar relaciones entre variables, como la relación entre un tratamiento y una respuesta biológica o la influencia de factores sociales en la salud.

Introducción a los Modelos Lineales

¿Qué es un Modelo Lineal?

Un modelo lineal es una herramienta matemática que describe la relación entre una o más variables predictoras (también llamadas variables independientes o explicativas) y una variable respuesta (también conocida como variable dependiente). Estos modelos son ampliamente utilizados en estadística y ciencia de datos porque permiten hacer predicciones, interpretar relaciones y entender los efectos de diferentes variables sobre un resultado de interés.

Una variable predictora es una variable que se utiliza para predecir o explicar la variabilidad en otra variable (la variable de respuesta). Por ejemplo, en un modelo que predice el rendimiento académico de los estudiantes, las variables predictoras podrían ser el tiempo de estudio, la asistencia a clases y el nivel socioeconómico.

En su forma más simple, un modelo lineal busca ajustar una línea recta a los datos, de manera que exprese cómo cambia la variable de interés a medida que cambian las variables predictoras. La linealidad del modelo implica que el impacto de cada predictor sobre la variable de interés es constante y puede ser representado por una pendiente (o coeficiente) en la ecuación de la línea recta. Esto quedará más claro cuando construyamos un modelo lineal en R.

Estructura del Modelo Lineal

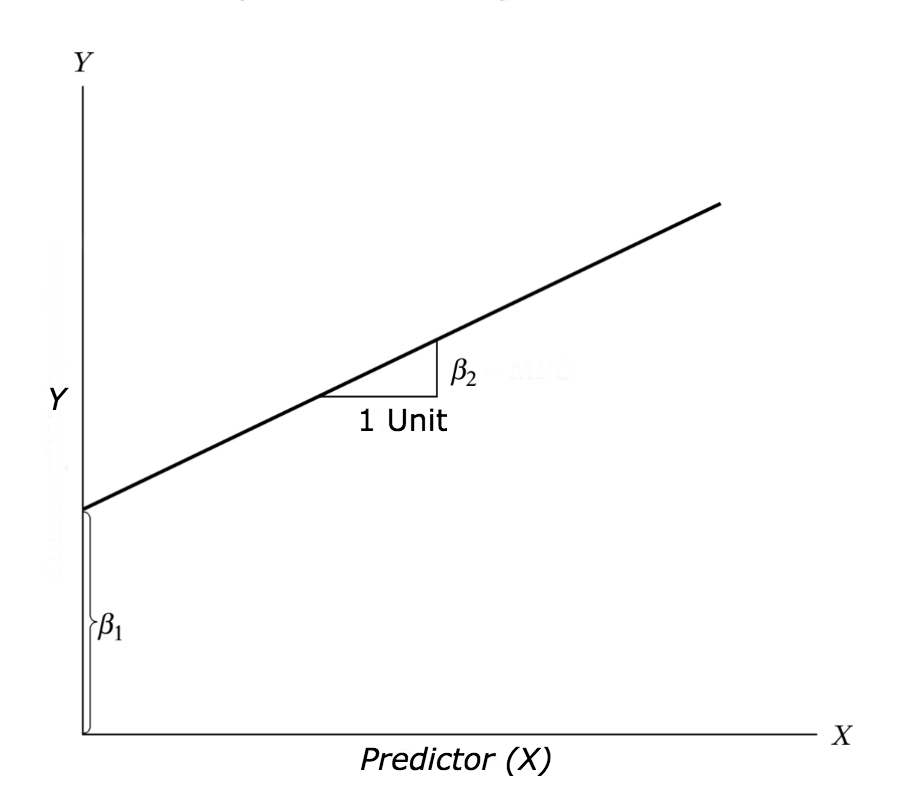
Matemáticamente, un modelo lineal simple para una variable predictora \((x)\) y una variable de respuesta \((y)\) se expresa como (observa que es una ecución de una recta, pero con un término de error que veremos más adelante):

\[ y = \beta_0 + \beta_1 \cdot x + \epsilon \]

\(y\) es la variable respuesta o dependiente.
\(\beta_0\) es el intercepto o término constante, que representa el valor promedio de \(y\) cuando \(x = 0\).
\(\beta_1\) es la pendiente o el coeficiente de regresión, que mide el cambio en \(y\) por cada unidad de cambio en \(x\).
\(\epsilon\) es el término de error o residuo, que captura las variaciones de \(y\) no explicadas por el modelo lineal.

Vamos a visualizar un modelo lineal simple con un ejemplo práctico en R.

Este modelo es lineal porque la relación entre \(x\) y \(y\) está representada por una relación lineal.

Explora cómo cambia la línea recta al modificar los valores de los coeficientes \(\beta_0\) y \(\beta_1\) en el modelo lineal. ¿Qué sucede con la pendiente y la intersección de la línea? ¿Cómo afecta esto a la relación entre \(x\) y \(y\)? Para cambiar los valores, haz click con tu mouse y arrastra los valores de 5 y 2 en la siguiente parte. El gráfico se actualizará automáticamente para que observes los cambios.

\(\beta_0=\) (Intercepto)
\(\beta_1=\) (Pendiente)

import {Tangle} from "@mbostock/tangle"

// Setup Tangle reactive inputs
viewof mean = Inputs.input(5); // Input for intercept (beta_0)
viewof sd = Inputs.input(2);   // Input for slope (beta_1)
meanTgl = Inputs.bind(Tangle({min: -10, max: 10, minWidth: "1em", step: 0.1}), viewof mean); // Intercept control
sdTgl = Inputs.bind(Tangle({min: -5, max: 5, minWidth: "1em", step: 0.1}), viewof sd);       // Slope control

// draw plot in R
draw_plot_lineal(mean, sd)

Interpretación de los Coeficientes del Modelo

Uno de los aspectos más útiles de los modelos lineales es la interpretación directa de los coeficientes (\(\beta_0, \beta_1\)):

Intersección (\(\beta_0\)): Representa el valor promedio de la variable respuesta \(y\) cuando todas las variables predictoras son iguales a cero. En muchos casos, esto tiene un significado concreto (por ejemplo, un valor base o inicial).
Pendiente (\(\beta_1\)): Nos dice en cuánto cambiará \(y\) si \(x\) aumenta en una unidad.

Important

Antes de seguir con las siguientes lecciones, observa este ejemplo con datos reales para entender cómo se ajusta un modelo lineal a los datos y cómo interpretar los coeficientes del modelo.
Vamos a regresar al ejemplo del módulo pasado de los pinguinos de Palmer. Primero, vamos a hacer el gráfico de dispersión de las variables masa_corporal_g y largo_aleta_mm para visualizar la relación entre ellas. Por el momento no vamos a dividir los datos por especie, sino que vamos a considerar todos los datos juntos.

Ahora, vamos a ajustar un modelo lineal simple a estos datos para predecir la longitud del pico a partir de la masa corporal.
En r, podemos lograr esto facilmente con la función geom_smooth() de ggplot2. Esta función ajusta un modelo lineal a los datos y muestra la línea de regresión en el gráfico de dispersión.
Observa que geom_smooth toma el argumento method = "lm", que indica que queremos ajustar un modelo lineal a los datos. Este modelo será ajustado con la fórmula y ~ x, donde y es la variable dependiente y x es la variable independiente (estos datos los toma de los argumentos x y y de aes()). El argumento se = FALSE indica que no queremos mostrar el intervalo de confianza alrededor de la línea de regresión (esto se verá en otro módulo).

Observa la línea roja en el gráfico de dispersión. Esta línea representa el modelo lineal ajustado a los datos. La intersección de la línea con el eje y es el valor de \(\beta_0\) (intercepto) y la pendiente de la línea es el valor de \(\beta_1\) (pendiente). En este caso, la pendiente nos dice cuánto aumenta la longitud del pico por cada gramo de masa corporal.
Si quisieras obtener los valores de los coeficientes (intercepto y pendiente) del modelo lineal ajustado (la linea roja), puedes usar la función lm() de R. Esta función ajusta un modelo lineal (linear model) a los datos y te da acceso a los coeficientes del modelo utilizando la función coef(modelo). Por ejemplo, para ajustar un modelo lineal a los datos de masa corporal y longitud del pico, puedes hacer lo siguiente:

El resultado es:

> coeficientes
    (Intercept) masa_corporal_g 
   136.72955927      0.01527592

donde el valor de Intercept es el valor de \(\beta_0\) y el valor de masa_corporal_g es el valor de \(\beta_1\). Esto significa que la longitud del pico aumenta en promedio 0.015 mm por cada gramo de masa corporal.

Resumen

Los modelos lineales son una herramienta matemática fundamental en estadística y ciencia de datos para describir la relación entre variables predictoras y una variable de respuesta.
Un modelo lineal simple se ajusta a los datos mediante una línea recta, donde la pendiente y el intercepto representan la relación entre las variables.
La interpretación de los coeficientes del modelo lineal es directa: la pendiente nos dice cuánto cambia la variable de respuesta por cada unidad de cambio en la variable predictora, y el intercepto es el valor promedio de la variable de respuesta cuando la variable predictora es cero.
Los modelos lineales son una base sólida para comprender y aplicar pruebas estadísticas comunes, como el t-test, ANOVA, regresión logística y más.