Comparación de Tres o Más Medias: ANOVA y Test de Kruskal-Wallis

Author

Affiliation

Mtro. Santiago Ríos

ANOVA y Test de Kruskal-Wallis

Introducción a los ANOVAs y el Test de Kruskal-Wallis

El análisis de varianza (ANOVA) es una herramienta estadística poderosa para comparar las medias de tres o más grupos.
Como hemos visto en las pruebas t para dos grupos, ANOVA se basa en el concepto de modelos lineales, extendiendo la idea de la codificación dummy para incluir más de dos grupos.
Debido a su importancia y extendido uso en la investigación (para bien o para mal), tendremos un módulo entero dedicado a este tema.

ANOVA unidireccional (One-way ANOVA): Evalúa si hay diferencias significativas entre las medias de tres o más grupos. Se basa en un modelo lineal que incluye términos de intersección ($(\beta_0$)) y pendientes ($(\beta_1, \beta_2, \dots$)) que representan las diferencias entre los grupos.
Test de Kruskal-Wallis: Es una alternativa no paramétrica al ANOVA unidireccional, que compara las distribuciones de tres o más grupos utilizando los rangos de los valores en lugar de los valores originales.

Ambas pruebas se basan en modelos lineales con codificación dummy, lo que nos permite analizar cómo las diferencias entre los grupos afectan la variable dependiente $(y$).

Puntos clave:

ANOVA unidireccional como modelo lineal: El modelo lineal en este caso predice la media de la variable dependiente ($(y$)) para cada grupo, utilizando variables indicadoras ($(x_0, x_1, x_2, $dots$)) que toman el valor de 0 o 1, dependiendo del grupo al que pertenece cada observación.

$[ y = \beta_0 + \beta_1 \cdot x_1 + \beta_2 \cdot x_2 + \dots$]
- Si $(x_1 = 1$), el modelo predice la media del primer grupo ($(\beta_0$)).
- Si $(x_2 = 1$), el modelo predice la media del segundo grupo ($(\beta_0 + \beta_1$)), y así sucesivamente.
Test de Kruskal-Wallis como modelo lineal: Similar al ANOVA, pero en lugar de los valores originales de $(y$), se utilizan los rangos de $(y$):

$[ \text{rango}(y) = \beta_0 + \beta_1 \cdot x_1 + \beta_2 \cdot x_2 + \dots$]

Este test es útil cuando los datos no cumplen con los supuestos de normalidad o contienen valores atípicos.
Codificación dummy: Al igual que en las pruebas t para dos grupos, la codificación dummy se utiliza para representar grupos categóricos como variables numéricas (0 o 1), lo que permite incluir múltiples grupos en un modelo lineal.

Observa en el siguiente gráfico que el ANOVA es “más de lo mismo” que hemos estado viendo en las pruebas t para dos grupos, pero extendido a tres o más grupos. La idea es la misma: comparar las medias de los grupos y ver si hay diferencias significativas:

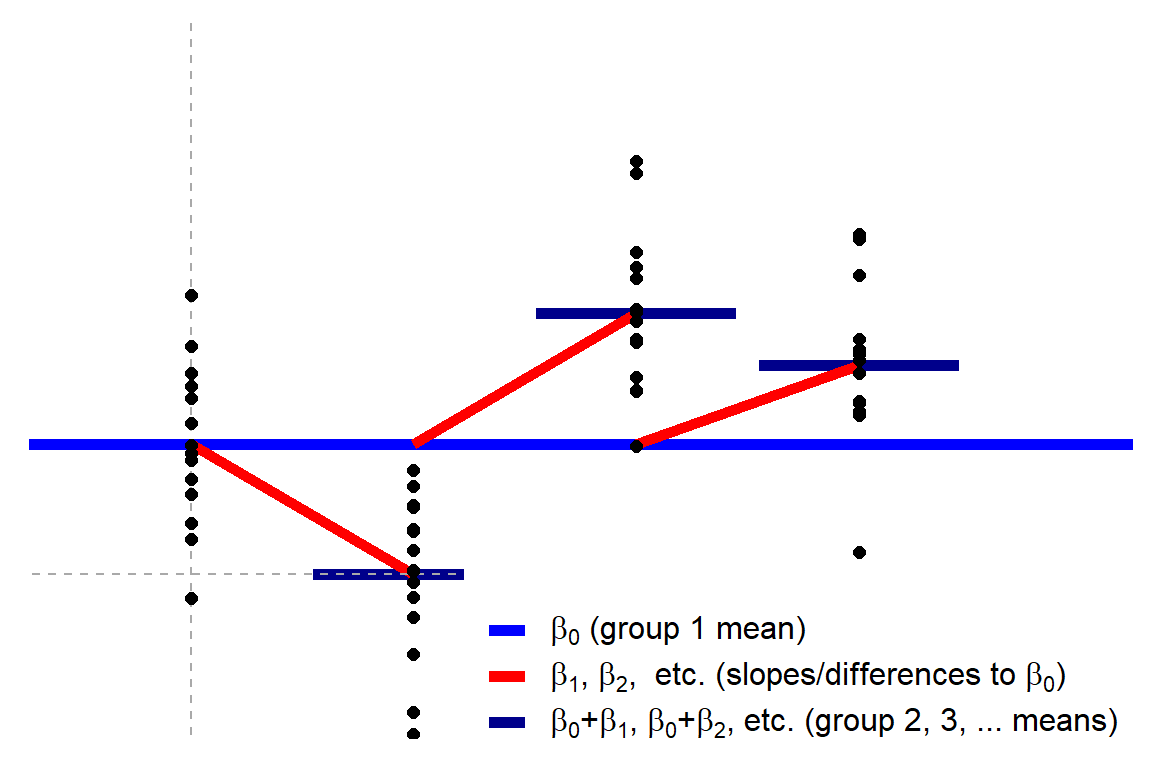
¿Por qué ANOVA y no pruebas t múltiples?

El ANOVA se basa en comparar la varianza (o variación) entre los grupos con la variación dentro de cada grupo en particular.
Si la variación “entre” es mucho mayor que la variación “dentro”, es más probable que concluyamos que las medias de los diferentes grupos no son iguales.
- entre o between se refiere a la variación entre los grupos, mientras que dentro o within se refiere a la variación dentro de cada grupo en particular.
Por el contrario, si las variaciones “entre” y “dentro” son más similares, es menos probable que concluyamos que existe una diferencia significativa entre las medias de las muestras.

¿Por qué no simplemente comparamos las medias de cada par posible de grupos para ver si existen diferencias estadísticamente significativas? - La razón es que al aumentar el número de grupos, es más probable que observemos diferencias que se deben únicamente al azar. - Esto significa que tenemos una mayor probabilidad de cometer un error Tipo I, es decir, rechazar la hipótesis nula (que no hay diferencia entre las medias) cuando, de hecho, la hipótesis nula es verdadera (siguiente tema del curso). - Un ANOVA controla este riesgo adicional de errores Tipo I, manteniendo la tasa de error global o del experimento, que típicamente es $\alpha$ = 0.05.

Es importante señalar que el ANOVA de una vía es una estadística de prueba global y no puede indicar qué grupos específicos fueron significativamente diferentes entre sí, solo que al menos dos grupos fueron diferentes. Para determinar qué grupos específicos difieren unos de otros, necesitarías utilizar una prueba post hoc.

ANOVA de dos vías

El ANOVA de dos vías compara las medias de grupos que se han dividido según dos variables independientes, o ‘factores’.

Por ejemplo: ¿existe una interacción entre el género y el nivel educativo en la ansiedad ante los exámenes entre estudiantes universitarios? Aquí, el género (masculino / femenino) y el nivel educativo (secundaria / pregrado / posgrado) son tus variables independientes o factores.

Un ANOVA de dos vías evalúa tres hipótesis:

Que las medias poblacionales del primer factor (por ejemplo, cada género) son iguales.
Que las medias poblacionales del segundo factor (por ejemplo, cada nivel educativo) son iguales.
Que no hay interacción entre los dos factores, es decir, que la relación entre la ansiedad y el género no depende del nivel educativo, o que la relación entre la ansiedad y la educación no depende del género.

Las dos primeras hipótesis se refieren a la relación entre cada factor y la variable dependiente, conocidas como ‘efectos principales’. Cada una de estas es similar a un ANOVA de una vía, pero en el contexto de un modelo más grande. La tercera hipótesis se refiere al ‘efecto de interacción’.

No complicaremos haciendo toda la demostración de nuevo. Si ya entendiste las pruebas t, entenderás el ANOVA. Y si ya entendiste la regresión lineal, entenderás el ANOVA. Es más de lo mismo, pero con más grupos. De nuevo, veremos ANOVA en detalle en un módulo posterior.