Visualización de Datos II

Otras formas de visualizar la distribución de datos

Además de los histogramas, los cuales representan la distribución de una variable continua dividiendo los datos en intervalos, existen otras formas de visualizar la distribución de datos. Dependiendo de la naturaleza de los datos y el objetivo de la visualización, es posible utilizar distintos gráficos para explorar y comunicar patrones en los datos.

Introducción

Para esta lección, seguiremos utilizando el paquete ggplot2 en R para crear visualizaciones avanzadas de datos.
Usaremos el juego de datos pinguinos que utilizamos en el módulo pasado, que contiene información sobre tres especies de pingüinos: Adelia, Papúa y Barbijo.
Primero, carguemos las librerías necesarias y exploremos el conjunto de datos.

El conjunto de datos pinguinos contiene las siguientes variables:

Variable Name	Description
`especie`	Especie de pingüino
`isla`	Isla donde se encontró el pingüino
`largo_pico_mm`	Longitud del pico en milímetros
`alto_pico_mm`	Profundidad del pico en milímetros
`largo_aleta_mm`	Longitud de la aleta en milímetros
`masa_corporal_g`	Masa corporal en gramos
`sexo`	Sexo del pingüino
`anio`	Año de la medición

Definir un tema global para ggplot

Como ya vimos, podemos usar temas de ggplot para personalizar la apariencia de nuestros gráficos.
Para no tener que estar especificando el tema en cada gráfico, podemos definir un tema global que se aplique a todos los gráficos que creemos.
Además, esto nos permite mantener la consistencia en la apariencia de nuestros gráficos.
Para esto, usamos la función theme_set() y especificamos el tema que queremos aplicar. Por ejemplo, vamos a aplicar el tema clásico a todos nuestros gráficos con este código (el código se ejecuta automáticamente al cargar esta página):

Puedes conocer más sobre los temas de ggplot en la este enlace.

Histogramas y gráficos de densidad

Recordemos cómo hacer un histogramas, los cuales son una forma común de visualizar la distribución de una variable continua.
A continuación, crearemos un histograma de la masa corporal de los pingüinos.

La mayoría de las veces, nos interesa ver cómo se distribuyen los datos en función de una variable categórica.
Por ejemplo, podemos querer comparar la distribución de la masa corporal de los pingüinos en cada una de las 3 especies del juego de datos.
Para esto, podemos usar la función de ggplot facet_grid() para dividir el gráfico en paneles según la variable categórica especie. Observa que utilizamos el operador ~ para indicar que queremos dividir el gráfico por la variable especie.

Otra forma de visualizar la distribución de una variable continua es mediante un gráfico de densidad.
Estos gráficos son similares a los histogramas, pero en lugar de dividir los datos en intervalos, muestran la distribución de los datos como una curva suave.
En estos gráficos, en lugar de representar la frecuencia de los datos, se muestra la densidad de probabilidad de los datos. El área bajo la curva es igual a 1 ya que representa la probabilidad total de los datos.
Ahora, en lugar de usar la función geom_histogram(), usaremos la función geom_density() para crear un gráfico de densidad de la masa corporal de los pingüinos.

En este tipo de gráficos, podemos decirle a ggplot que divida los datos en función de una variable categórica, de manera similar a lo que hicimos con los histogramas.
Podríamos usar de nuevo la función facet_grid() para dividir el gráfico en paneles según la variable categórica especie. Sin embargo, en este caso, usaremos la función fill para colorear las curvas de densidad según la variable categórica especie.
En este caso, no vamos a dividir el gráfico en paneles, sino que vamos a superponer las curvas de densidad de las tres especies de pingüinos en un solo gráfico para compararlas facilmente. Para facilitar la comparación, observa que pasamos el argumento alpha = 0.5 a la función geom_density() para hacer las curvas semitransparentes. alpha controla la transparencia de los elementos del gráfico, con 0 siendo completamente transparente y 1 siendo completamente opaco.

Comparación entre geom_histogram() y geom_density()

Característica	geom_histogram()	geom_density()
Tipo de gráfico	Barras que muestran la frecuencia de los datos en intervalos	Curva suave de densidad de probabilidad
Representación	Frecuencia absoluta (o densidad si se normaliza) por intervalo	Densidad de probabilidad continua
Ajuste o suavizado	Depende del número de bins o del ancho de los bins	Estimador de densidad kernel (KDE)
Flexibilidad	Depende de la elección de los bins	Más flexible y suave, no depende de intervalos
Interpretación	Frecuencia de los datos en grupos específicos	Tendencia general de la distribución de los datos

Tips para graficar histogramas y densidades

Sobreponer histograma y densidad

En ocasiones, es útil superponer un histograma y una gráfica de densidad para comparar la distribución de los datos de manera más efectiva.
Esto puede ayudarte a visualizar la forma de la distribución y cómo se ajusta la densidad a los datos observados en el histograma.
Para hacer esto, simplemente agregamos las dos capas al gráfico utilizando geom_histogram() y geom_density().
Observa que usamos el argumento aes(y = ..density..) en geom_histogram(). Esto es para normalizar el histograma, de manera que su altura sea comparable con la curva de densidad generada por geom_density(). Es decir, en lugar de mostrar la frecuencia absoluta (número de observaciones en cada intervalo), normalizamos el histograma para que la suma de las alturas de las barras sea igual a 1, lo que permite comparar la forma de la distribución con la curva de densidad.
Otro argumento nuevo que aparece en este código es position = "identity dentro de geom_histogram(). Este argumento especifica cómo se deben posicionar los elementos gráficos (como barras, puntos, líneas, etc.) cuando hay superposición de datos. El argumento position = “identity” le dice a ggplot2 que no ajuste la posición de los elementos gráficos y que los dibuje en su ubicación original, es decir, en el mismo lugar donde los datos pertenecen. Esto es especialmente útil cuando quieres superponer varias capas de gráficos, como un histograma y una curva de densidad, o cuando estás comparando varias categorías en un mismo gráfico. Cuando tienes múltiples grupos o categorías, por defecto, ggplot2 trata de ajustar la posición de los elementos gráficos para que no se superpongan completamente.
Otros argumentos de posición son: “stack” (apila los elementos), “dodge” (distribuye los elementos uno al lado del otro), “fill” (apila los elementos y los rellena), “jitter” (agrega un poco de ruido a los elementos para evitar la superposición), entre otros. Algunos de estos ejemplos irán apareciendo en lecciones futuras.

Visualizar la media en un histograma

En ocasiones, es útil visualizar la media de una variable en un histograma para tener una idea de la ubicación central de los datos.
Para hacer esto, podemos agregar una línea vertical al histograma que represente la media de los datos.
En el siguiente código, calculamos la media de la masa corporal de los pingüinos y la agregamos al histograma utilizando la función geom_vline().
Observa que geom_vline() tiene los siguientes argumentos: xintercept (la posición en el eje x donde se dibujará la línea vertical), color (el color de la línea), linetype (el tipo de línea, puede ser “solid”, “dashed”, “dotted”, entre otros) y size (el grosor de la línea).
El argumento aes(xintercept = mean(masa_corporal_g, na.rm = TRUE)) calcula directamente la media de masa_corporal_g dentro de ggplot. El parámetro na.rm = TRUE asegura que se ignoren los valores faltantes (NA).

Boxplots y Violin Plots

Boxplots

Los boxplots y los violin plots son gráficos que permiten visualizar la distribución de una variable continua en función de una variable categórica.
Los boxplots son gráficos que muestran la distribución de los datos a través de sus cuartiles y resaltan valores atípicos.
Cuartil: Un cuartil es un valor que divide un conjunto de datos ordenados en cuatro partes iguales. El primer cuartil (Q1) es el valor que deja el 25% de los datos por debajo, el segundo cuartil (Q2) es la mediana y el tercer cuartil (Q3) es el valor que deja el 75% de los datos por debajo. En una distribución normal, la mediana es igual a Q2.
Valor atípico: Un valor atípico es un valor que es significativamente diferente del resto de los datos en un conjunto. En un boxplot, los valores atípicos se representan como puntos individuales fuera de los “bigotes” del gráfico. Estos puntos, también llamados outliers, son valores que caen fuera de 1.5 veces el rango intercuartílico (IQR) por encima del tercer cuartil o por debajo del primer cuartil y pueden ser indicativos de errores en los datos o de fenómenos inusuales. Dependiendo del contexto, los valores atípicos pueden ser eliminados, transformados o analizados en detalle.

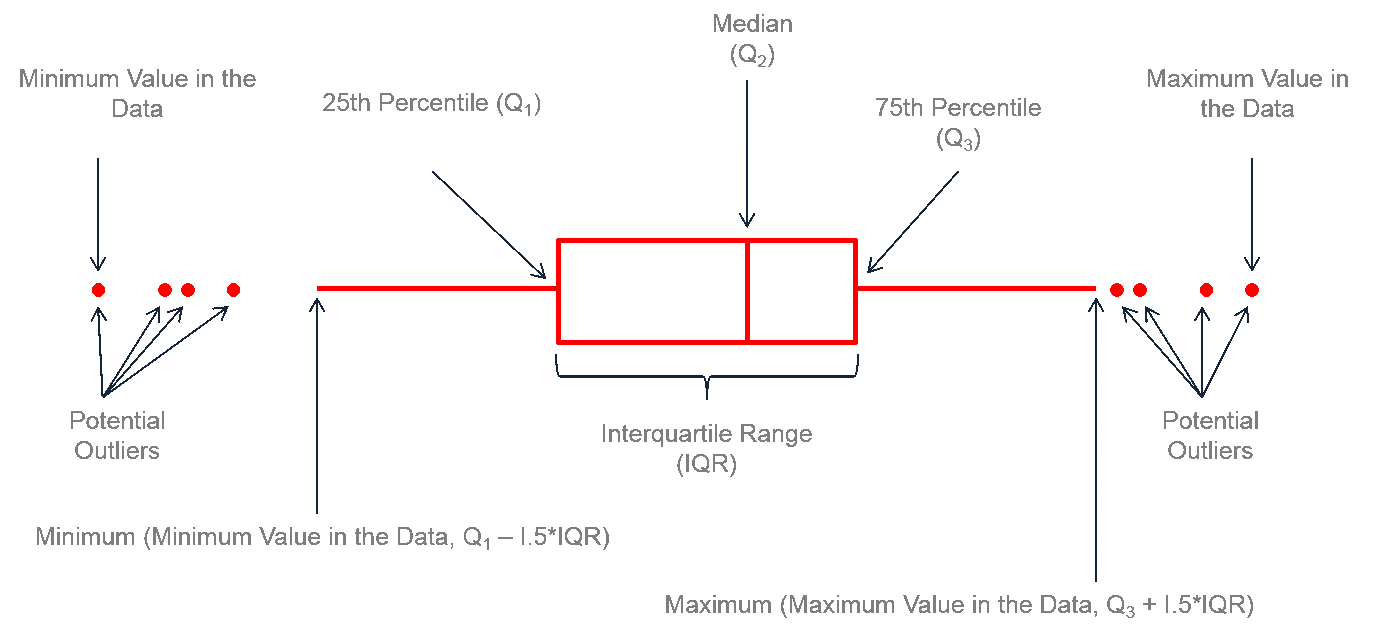
Mediana: La línea dentro de la caja representa la mediana de la distribución.
Cuartiles: Los extremos de la caja muestran el primer cuartil (Q1) y el tercer cuartil (Q3), es decir, el 25% y el 75% de los datos.
Rango intercuartílico (IQR): Es el rango entre Q1 y Q3, y la longitud de la caja representa este rango.
Bigotes (whiskers): Se extienden hasta 1.5 veces el IQR desde los cuartiles. Más allá de estos bigotes, los puntos se consideran valores atípicos.
Valores atípicos (outliers): Los puntos individuales que caen fuera de los bigotes se consideran atípicos y se muestran como puntos.
Para crear un boxplot en ggplot, usamos la función geom_boxplot().
Como vamos a ver la distribución de una variable contínua (masa_corporal_g) en función de una variable categórica (en este caso especie), usaremos aes(x = especie, y = masa_corporal_g) para mapear las variables al gráfico.

Observa que la caja de nuestro boxplot se ve dividida en tres partes: la línea en el medio de la caja representa la mediana. Como nuestros datos están distribuídos aproximadamente de manera normal, la mediana divide los datos en dos partes iguales. Si los datos no están distribuídos de manera normal, la mediana no necesariamente divide los datos en dos partes iguales.
Además, podemos ver la dispersión de las masas en las 3 especies. Esta dispersión se observa en la extensión del del boxplot, que representan el rango de los datos. Por lo tanto, una variable con alta dispersión tendrá un boxplot más largo.
Observa que la especie “Barbijo” tiene 2 valores atípicos, representados como puntos individuales fuera de los “bigotes” del gráfico.
Rápidamente podemos ver que la especie Papua tiene una mediana de masa más alta que las otras dos especies. Sin embargo, esta no es una comparación formal de las medias. Para esto, necesitaríamos realizar un análisis estadístico como una prueba t o un análisis de varianza (ANOVA) que se verán más adelante en el curso.

Violín

Ahora, un gráfico de violín es una forma de visualizar la distribución de los datos que combina aspectos del boxplot y el gráfico de densidad.
La forma del “violín” muestra la densidad de los datos en varios puntos a lo largo del eje y, lo que permite ver dónde se encuentran la mayoría de los datos (zonas más anchas) y las zonas menos densas (zonas más estrechas).
También podemos ver la simetría de nuestros datos: si el gráfico de violín es simétrico, significa que tenemos aproximadamente la misma densidad en ambos lados.
A diferencia del boxplot, que solo muestra un resumen de los datos, el gráfico de violín te permite ver la forma completa de la distribución.

Puedes pensar en un gráfico de violín como un histograma girado 90 grados y reflejado a lo largo del eje y, por ejemplo:

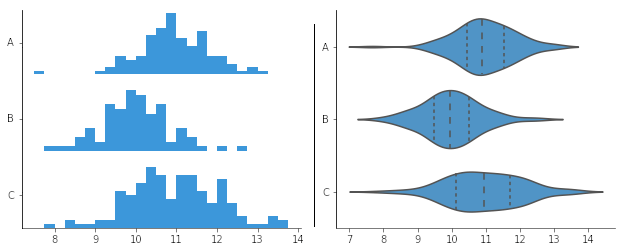
Adicionalmente, es una forma más visual de comparar la distribución de los datos entre diferentes categorías cuando tenemos muchos datos.
Por ejemplo, observa que es más fácil comparar la distribución de la masa corporal entre las diferentes especies de pingüinos divididos por isla y sexo en un solo gráfico. En este caso, usamos facet_grid(~ isla) para dividir el gráfico en paneles según la variable categórica isla y fill = sexo para colorear los violines según la variable categórica sexo.

Resumen

Comparación entre geom_boxplot() y geom_violin()

Característica	`geom_boxplot()`	`geom_violin()`
Resumen de datos	Mediana, cuartiles, valores atípicos	Densidad de los datos, opcionalmente mediana y cuartiles
Distribución completa	No muestra la distribución completa, solo un resumen	Muestra la distribución completa, incluyendo densidades
Valores atípicos	Los muestra explícitamente	No se muestran explícitamente, pero puedes añadir un boxplot
Ventajas	Sencillo, compacto, destaca valores atípicos	Muestra la forma completa de la distribución, útil para datos complejos
Cuándo usar	Comparaciones simples entre grupos, detección de outliers	Comparación de la distribución general, especialmente si es multimodal

¿Cuándo usar cada uno?

Usar geom_boxplot(): - Cuando necesitas un resumen claro y conciso de la distribución que incluya la mediana, los cuartiles y los valores atípicos. - Cuando quieres comparar varios grupos de manera rápida y eficiente. - Cuando estás interesado en la variabilidad y los valores atípicos, porque los boxplots destacan los outliers de forma clara.

Usar geom_violin(): - Cuando te interesa la forma general de la distribución de los datos, no solo un resumen. - Cuando sospechas que los datos tienen una distribución compleja, por ejemplo, si es multimodal (con varios picos) o asimétrica. - Cuando quieres comparar densidades entre grupos y ver dónde se concentra la mayor parte de los datos. - Si prefieres una visualización más detallada y estética que muestre la forma completa de los datos.

Ver asociaciones entre 2 variables continuas

Hasta ahora, hemos visto cómo visualizar la distribución de una variable continua en función de una variable categórica.
Ahora, vamos a explorar cómo visualizar la relación entre dos variables continuas, como la masa corporal y la longitud de la aleta de los pingüinos.
Un gráfico de dispersión es una herramienta útil para visualizar la relación entre dos variables cuantitativas. En este tipo de gráfico, cada punto representa una observación, con una variable en el eje x y otra en el eje y. Por ejemplo, si tenemos datos de animales, como altura y peso, podemos usar un gráfico de dispersión para explorar si existe una relación entre estas dos variables.
Para crear un gráfico de dispersión en ggplot, usamos la función geom_point() y mapeamos las variables al eje x y y. Toma el argumento de size para controlar el tamaño de los puntos y el argumento alpha para controlar la transparencia de los puntos.
Vamos a explora la relación entre el largo de la aleta y la masa corporal de los pinguinos.

Este gráfico te permite explorar si existe alguna relación entre la masa corporal y la longitud de aleta de los pingüinos.
Podemos ver muy claramente que en todas las especies, la masa corporal y la longitud de aleta están positivamente correlacionadas: a medida que la masa corporal aumenta, también lo hace la longitud de aleta.
Este concepto será importante cuando exploremos correlaciones y regresiones en lecciones futuras ya que nos permitirá entender cómo dos variables se relacionan entre sí.

Tip

Una forma fácil de explorar todas las relaciones entre variables continuas en un conjunto de datos es mediante un gráfico de pares.
En un gráfico de pares, se muestran todas las combinaciones posibles de gráficos de dispersión entre las variables continuas en un conjunto de datos.
Esto puede ser útil para identificar patrones y asociaciones entre las variables, en especial si tienes muchas variables continuas en tus datos.
Para esto vamos a usar la función ggpairs() del paquete GGally. Especificamos las columnas que queremos incluir en el gráfico de pares con el argumento columns.
Por el momento no te preocupes por el código ni los valores de correlación, simplemente observa cómo se ven las relaciones entre las variables en el gráfico de pares. En lecciones futuras, profundizaremos en cómo interpretar estos gráficos y cómo calcular correlaciones y regresiones.
A simple vista, ¿puedes identificar alguna relación entre las variables en el gráfico de pares? Observa cómo masa corporal y largo de aleta siguen un patrón muy claro, donde a medida que una variable aumenta, la otra también lo hace. También pon atención en la relación de alto_pico y largo_aleta, donde se observan dos grupos claramente diferenciados: uno con pinguinos de menor largo de aleta y mayor alto de pico (Adelia y Barbijo) y otro con pinguinos de mayor largo de aleta y menor alto de pico (Papúa). Otras relaciones como masa corporal y alto de pico no parecen tener una relación tan clara. Sin embargo, recuerda que estas son solo observaciones visuales y no análisis formales de correlación, las cuales veremos más adelante.

NOTA 1: Observa que en este gráfico especificamos un nuevo tema con + theme_bw(). A pesar de que al inicio especificamos un tema global, podemos cambiar el tema de un gráfico específico de esta forma. En este caso, usamos theme_bw() porque incorpora una cuadrícula de fondo que facilita la visualización de los gráficos de dispersión.
NOTA 2: En este gráfico de pares, cada celda muestra un gráfico de dispersión entre dos variables. La diagonal principal muestra un histograma de cada variable. Los valores en la parte inferior de cada celda son los coeficientes de correlación de Pearson entre las dos variables. Estos valores varían entre -1 y 1, donde -1 indica una correlación negativa perfecta, 1 indica una correlación positiva perfecta y 0 indica que no hay correlación. En lecciones futuras, veremos cómo interpretar estos valores y cómo calcular correlaciones y regresiones de manera más formal.

Conteos

Cuando estamos interesados en visualizar magnitudes asociadas a diferentes categorías (por ejemplo, las ventas de distintas marcas de autos o las poblaciones de diferentes ciudades), el gráfico más común es el gráfico de barras.
Este tipo de gráfico es ideal para mostrar cantidades asociadas a categorías, donde el enfoque principal es la magnitud de los valores numéricos.
En un gráfico de barras estándar, las alturas de las barras representan la cantidad, como el número de observaciones en cada categoría.
Existen varias variaciones de gráficos de barras, como las barras apiladas o agrupadas o el heatmap (mapa de calor) que se verán al final del curso.
En ggplot2, el gráfico de barras básico se puede crear con geom_bar(), que cuenta automáticamente las observaciones en cada categoría.
NOTA: Si quieres que las alturas de las barras representen un valor numérico específico (en lugar de contar observaciones), puedes usar geom_col(). geom_col() lo veremos más adelante ya que es un gráfico muy utilizado en pruebas estadísticas que comparan medias. Aquí nos enfocaremos en geom_bar() que solo cuenta observaciones.

Conteo automático en el eje Y: geom_bar() cuenta automáticamente el número de observaciones (pingüinos) en cada categoría.

Note

Solo como nota, si en lugar de contar las observaciones, quisieras mostrar un valor numérico específico (por ejemplo, el promedio de la masa corporal por especie), usaríamos geom_col(), que mapea explícitamente la altura de las barras a un valor numérico del dataset. Como se mencionó, esto se verá más adelante, pero aquí tienes un ejemplo de cómo se vería:

Comparación entre geom_bar() y geom_col(): - geom_bar(): Útil para mostrar el conteo de observaciones en cada categoría. Las barras representan el número de veces que ocurre cada categoría. Úsala cuando simplemente quieras contar cuántas observaciones pertenecen a cada categoría. - geom_col(): Se usa cuando quieres que las alturas de las barras representen un valor numérico específico, como una suma, un promedio u otra medida. Úsala cuando ya tienes valores calculados (por ejemplo, promedios, sumas) y quieres representarlos con barras.

EXTRA: Explora las variables de los pingüinos

Puedes continuar explorando la distribución de las distintas variables en las diferentes especies de pingüinos con este gráfico interactivo. Simplemente selecciona la variable que te interesa y las especie de pingüino que quieres explorar.

viewof species = Inputs.checkbox(
  [ "Adelia", "Barbijo", "Papúa" ],
  { value: ["Adelia", "Barbijo"], label: "Especies" }
);
viewof measure = Inputs.select(
  [ "largo_aleta_mm", "largo_pico_mm", "alto_pico_mm", "masa_corporal_g" ],
  { label: "Variables" }
);
do_penguins_density(measure, species);

Tip

El gráfico anterior es interactivo y está construido con una serie de funciones y programación condicional. En este caso, usamos la función do_penguins_density para crear un gráfico de densidad de una variable seleccionada en función de una especie de pingüino seleccionada. Este tipo de gráficos es más complejo y no se verá en el curso, pero sirve como muestra del poder de R en la visualización de datos. Les dejo el código aquí por si les interesa explorar más sobre cómo se construyó este gráfico. Aunque ahora puede que no lo entiendan del todo, verán que a medida que avancen en el curso, podrán entender y crear gráficos más complejos como este. Esta es la base de cómo se construyen aplicaciones de análisis de datos con R. En un futuro, habrá un curso de desarrollo de aplicaciones con R.

do_penguins_density <- function(measure, sp) {
  filtered <- pinguinos |> filter(especie == sp)
  ggplot(data = filtered, aes(x = .data[[measure]])) +
  geom_density(aes(fill = especie), alpha = 0.8, position = "identity") +
  labs(title = "Penguins 🐧")
}

//| echo: false
viewof species = Inputs.checkbox(
  [ "Adelia", "Barbijo", "Papúa" ],
  { value: ["Adelia", "Barbijo"], label: "Especies" }
);
viewof measure = Inputs.select(
  [ "largo_aleta_mm", "largo_pico_mm", "alto_pico_mm", "masa_corporal_g" ],
  { label: "Variables" }
);
do_penguins_density(measure, species);