Distribuciones de Probabilidad

Distrbución Normal

Author

Affiliation

Mtro. Santiago Ríos

Introducción y Objetivos

Antes de comenzar con las lecciones de estadística, es importante entender las distribuciones de probabilidad.
Las distribuciones de probabilidad describen cómo se distribuyen los valores posibles de una variable aleatoria. Estas representan la probabilidad de los valores que puede tomar una variable, siendo algunos valores más probables que otros.
Una variable aleatoria es una variable (lección previa) cuyos valores son el resultado de un fenómeno aleatorio, como el lanzamiento de un dado o la altura de un grupo de personas.
En las siguientes lecciones, abordaremos algunas de las distribuciones más comunes y cómo trabajarlas en R.
Para ello, nos enfocaremos en un ejemplo fictício de alturas de jirafas “miniatura” en 2 diferentes islas.

Imagina que tomas aleatoriamente la altura de 100 jirafas: 50 pertenecienctes a la isla A y 50 a la isla B, como se muestra en las imágenes.

Gráficos por tinystats.

¿Cómo podemos visualizar los 100 datos para ver cuál es la altura más común, la menos común y el rango de las alturas?
Una forma practica sería la siguiente: tomas la altura de cada jirafa y llevas un conteo de cuántas veces se repite cada altura (frecuencia).
Para simplificar este conteo, vamos a redondear las alturas a números enteros (por ejemplo, 6 cm, 7 cm, 8 cm, etc.).
Esta es la base de un gráfico conocido como histograma, que muestra la distribución de los datos. Como verás, hay valores que se repiten más que otros, lo que se observa como picos en el gráfico.
Ejecuta el código de la siguiente diapositiva y observa cómo se va construyendo el histograma. Cada “bolita” que aparece en el gráfico representa un dato de altura. Si hay más de un dato para esa altura, se apila para llevar el conteo o frecuencia. No te preocupes por el código, solo observa el gráfico.
NOTA: Puedes hacer click en el botón de reproducción (play) para ver la animación después de ejecutar el código; tarda unos segundos en cargar la animación.

Código usado para el gráfico de la distribución de alturas de jirafas

library(plotly)
library(tidyverse)
library(tweenr)

set.seed(12)
x <- round(rnorm(25, 10, 2))
x2 <- round(rnorm(25, 18, 1.2))
x <- c(x, x2)
df <- data.frame(x = x, y = 23, type = rep(c("Isla #1", "Isla #2"), each = 25))
dfs <- list(df)
for (i in seq_len(nrow(df))) {
  dftemp <- tail(dfs, 1)
  dftemp[[1]]$y[i] <- sum(dftemp[[1]]$x[seq_len(i)] == dftemp[[1]]$x[i])
  dfs <- append(dfs, dftemp)
}
dfs <- append(dfs, dfs[rep(length(dfs), 3)])
# Reduce nframes to 100
dft <- tween_states(dfs, tweenlength = 10, statelength = 1, ease = "cubic-in", nframes = 100)
dft$y <- dft$y - 0.5
dft <- dft[dft$y != 23, ]

m <- list(l = 50, r = 50, b = 10, t = 10, pad = 4)

histograma_plot <- 
  dft %>% 
  plot_ly(
    x = ~x, y = ~y, frame = ~.frame, color = ~type,
    colors = c("green3", "turquoise3"),
    marker = list(size = 16), width = 630, height = 390
  ) %>%
  config(displayModeBar = F) %>%
  layout(
    xaxis = list(range = c(4, 23), title = "Altura de jirafas en cm", zeroline = F),
    yaxis = list(range = c(-0.5, 21), title = "Frecuencia", zeroline = F),
    legend = list(x = 0.075, y = 0.91),
    autosize = F, margin = m
  ) %>%
  animation_opts(frame = 25, transition = 0, redraw = FALSE) %>%
  animation_slider(hide = T) %>%
  animation_button(x = 1, xanchor = "right", y = 0, yanchor = "bottom")

El grafico que acabamos de ver (histograma) muestra la distribución o forma de nuestros datos.
A partir de la distribución de nuestra variable de altura, podemos observar lo siguiente:
- Dónde se concentran la mayoría de los valores de altura para cada isla.
- La altura más común es diferente para las firafas de la isla 1 y 2.
- Hay una variabilidad en las alturas, con algunas jirafas más altas y otras más bajas.
Dependiendo de la forma de la distribución, se le da un nombre a esta distribución de los datos.
La más común y utilizada en ciencias biomédicas es la distribución normal, también conocida como campana de Gauss. Muchas variables en la naturaleza siguen una distribución normal, como la altura de las personas, el peso de los animales, la temperatura, etc. Sin embargo, no todas las variables siguen una distribución normal, por lo que es importante verificar la forma de la distribución de los datos antes de realizar cualquier análisis estadístico.
Observa el siguiente gráfico de la distribución normal, que muestra la forma típica de esta distribución. En lo que resta de la lección veremos las características de esta distribución y cómo se relaciona con nuestros datos de alturas de jirafas.

Cada distribución tiene sus propias características y propiedades, lo que las hace únicas y útiles para diferentes situaciones.
En el caso de la distribución normal, podemos describirla con dos parámetros: la media y la desviación estándar que se verán a continuación.
Exploremos la distribución normal con nuestro ejemplo de alturas de jirafas. Podemos observar las siguientes características:
- Tiene un solo pico o punto más alto donde se concentran los datos.
  - NOTA: En nuestro gráfico se observan 2 picos, pero esto es porque estamos observando las alturas de 2 grupos de jirafas diferentes. Sin embargo, cada grupo tiene un único pico.
- Los datos se distribuyen simétricamente alrededor de este punto medio.

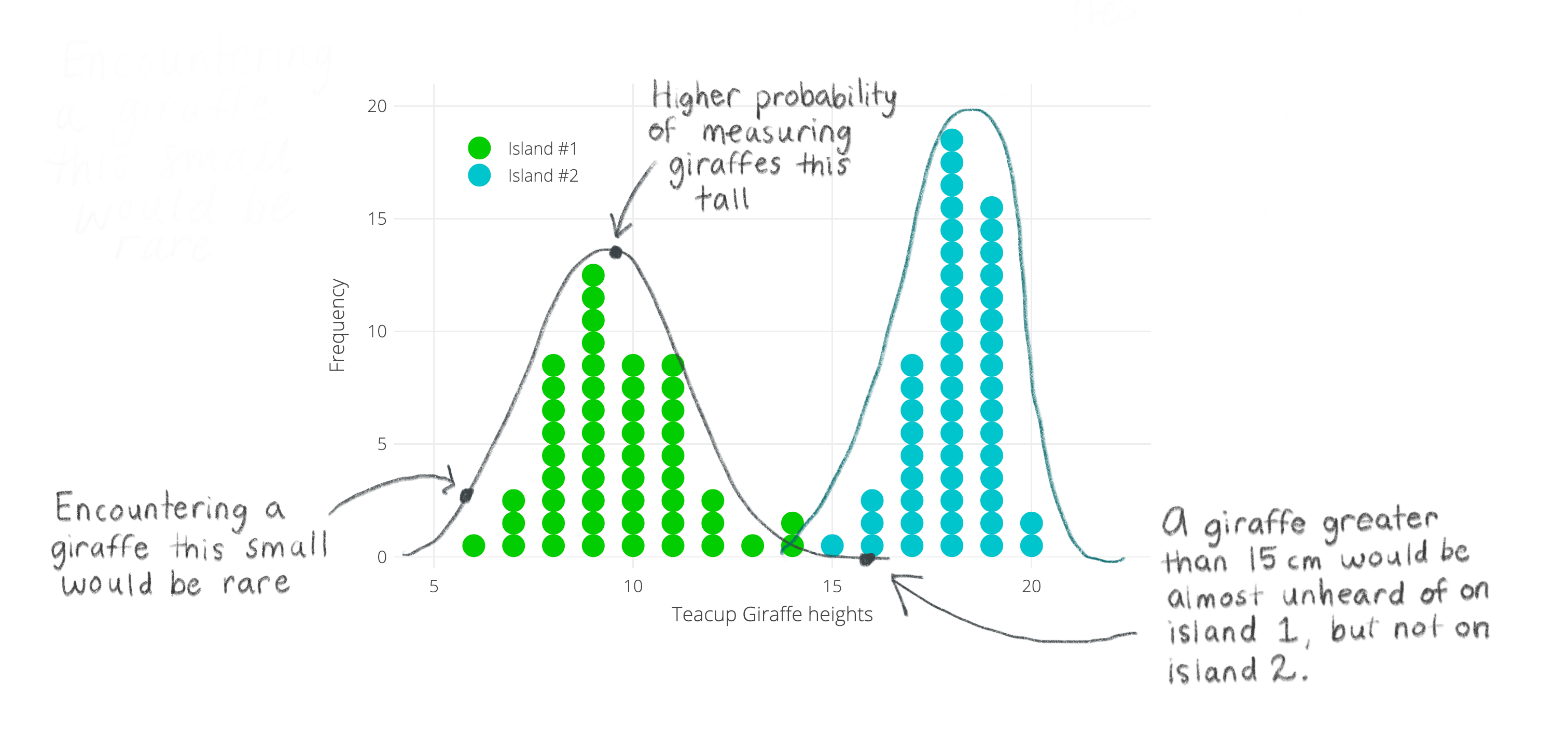
Una vez que hemos visualizado la distribución de los datos de nuestra variable, el siguiente paso es describir las alturas con medidas numéricas.
Para esto, utilizamos las medidas de tendencia central y dispersión.
Estas medidas nos ayudan a comprender tanto el “centro” de los datos como la “dispersión” de estos.

Medidas de Tendencia Central

Las medidas de tendencia central nos ayudan a resumir la “ubicación” de los datos, en especial, dónde se concentran los datos. Las medidas más comunes son:
- Media: el promedio de los datos.
- Mediana: el valor que se encuentra en el centro de los datos.
- Moda: el valor que se repite con mayor frecuencia.
En una distribución normal teórica, la media, mediana y moda son idénticas. Sin embargo, en la práctica, suelen ser diferentes, aunque cercanas.

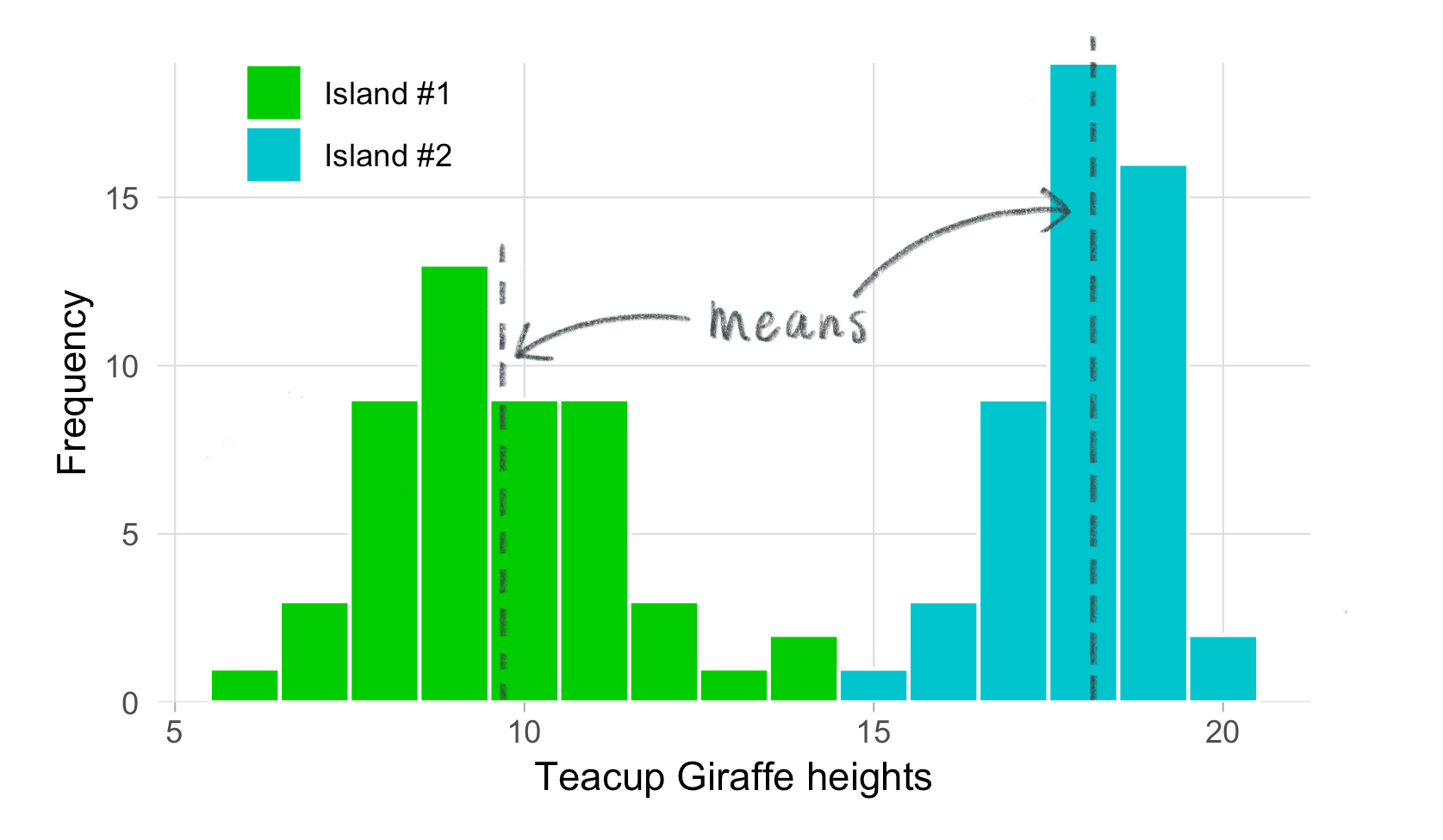
Media o Promedio

La media es el promedio de todos los valores en un conjunto de datos.
Se calcula sumando todos los valores y dividiendo por el número total de observaciones.
Puede ser calculada fácilmente en R con la función mean(), la cuál podemos usar denrtro de las funciones de manipulación de datos de dplyr como ya hemos visto.
Observa cómo calculmos la media de las alturas de las jirafas en el siguiente código. Nuestro dataframe se llama alturas_df (ya está cargado en la diapositiva) y tiene las columnas altura e isla.

Note

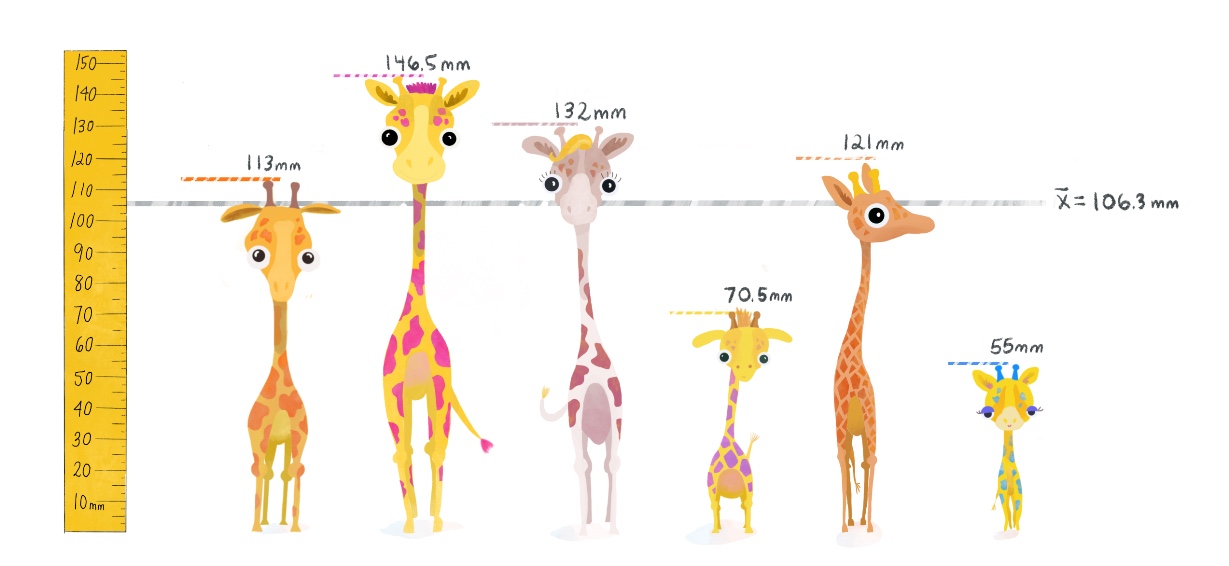
Cuando nos referimos a la media, podemos hablar de la media poblacional o la media muestral.
La media poblacional es el promedio de todos los valores en una población completa y se denota con el símbolo μ (mu). Esta media es desconocida en la práctica, ya que rara vez tenemos acceso a todos los datos de una población.
La media muestral es el promedio de los valores en una muestra de la población y se denota con el símbolo x̄ (x barra). Esta es la media que calculamos con nuestros datos.
De manera similar, cuando nos referimos al tamaño de la población, usamos N, y cuando nos referimos al tamaño de la muestra, usamos n (en nuestro caso, n = 100).

Podemos visualizar la media en nuestro histograma de alturas de jirafas. La línea vertical en el gráfico representa la media de las alturas de las jirafas en cada isla. Observa cómo la media se encuentra en el centro de la distribución de los datos. Nota: en la próxima lección veremos y explicaremos cómo realizar estos gráficos.

Mediana

La mediana es el valor que se encuentra en el centro de los datos cuando estos están ordenados de menor a mayor.
Es una medida de tendencia central robusta, ya que no se ve afectada por valores extremos o atípicos.
En R, podemos calcular la mediana con la función median().

Para graficarlo (observa que el valor de la mediana es muy similar al de la media):

Moda

La moda es el valor que se repite con mayor frecuencia en un conjunto de datos.
Puede haber más de una moda en un conjunto de datos, lo que se conoce como distribución multimodal.
En R, podemos calcular la moda con la función mode(). NOTA: esta función no está disponible en R por defecto, por lo que debemos definirla manualmente.

Medidas de Dispersión

Las medidas de dispersión nos ayudan a entender cuánto varían los datos (qué tan dispersos están).
En la siguiente figura, se muestran 3 distribuciones de probabilidad de una variable con la misma media pero diferente dispersión. La distribución de la izquierda tiene una menor dispersión que la del centro, aunque la figura de la derecha es la que menor dispersión tiene. Vamos a ver qué significa esto en términos de medidas de dispersión.

Varianza

La varianza mide cuánto varían los datos alrededor de la media.
Se calcula sumando las diferencias al cuadrado entre cada valor y la media, y luego dividiendo por el número total de observaciones.
La varianza es una medida de dispersión cuadrática, ya que considera la magnitud de las diferencias al cuadrado. Esto se hace para evitar que las diferencias positivas y negativas se cancelen entre sí.
En R, podemos calcular la varianza con la función var().

Note

Cuando se habla de varianza, también se puede hacer referencia a la varianza poblacional y la varianza muestral. La varianza poblacional es la varianza de todos los valores en una población completa y se denota con el símbolo \(\sigma^2\) (sigma al cuadrado). La varianza muestral es la varianza de los valores en una muestra de la población y se denota con el símbolo \(s^2\). En la práctica, usamos la varianza muestral, ya que rara vez tenemos acceso a todos los datos de una población.

Desviación Estándar

El problema con la varianza es que está en unidades al cuadrado, lo que puede ser difícil de interpretar. Por eso, a menudo usamos la desviación estándar, que es la raíz cuadrada de la varianza.
La desviación estándar mide cuánto se desvían los datos de la media, pero en las mismas unidades que los datos.
En R, podemos calcular la desviación estándar con la función sd().

Note

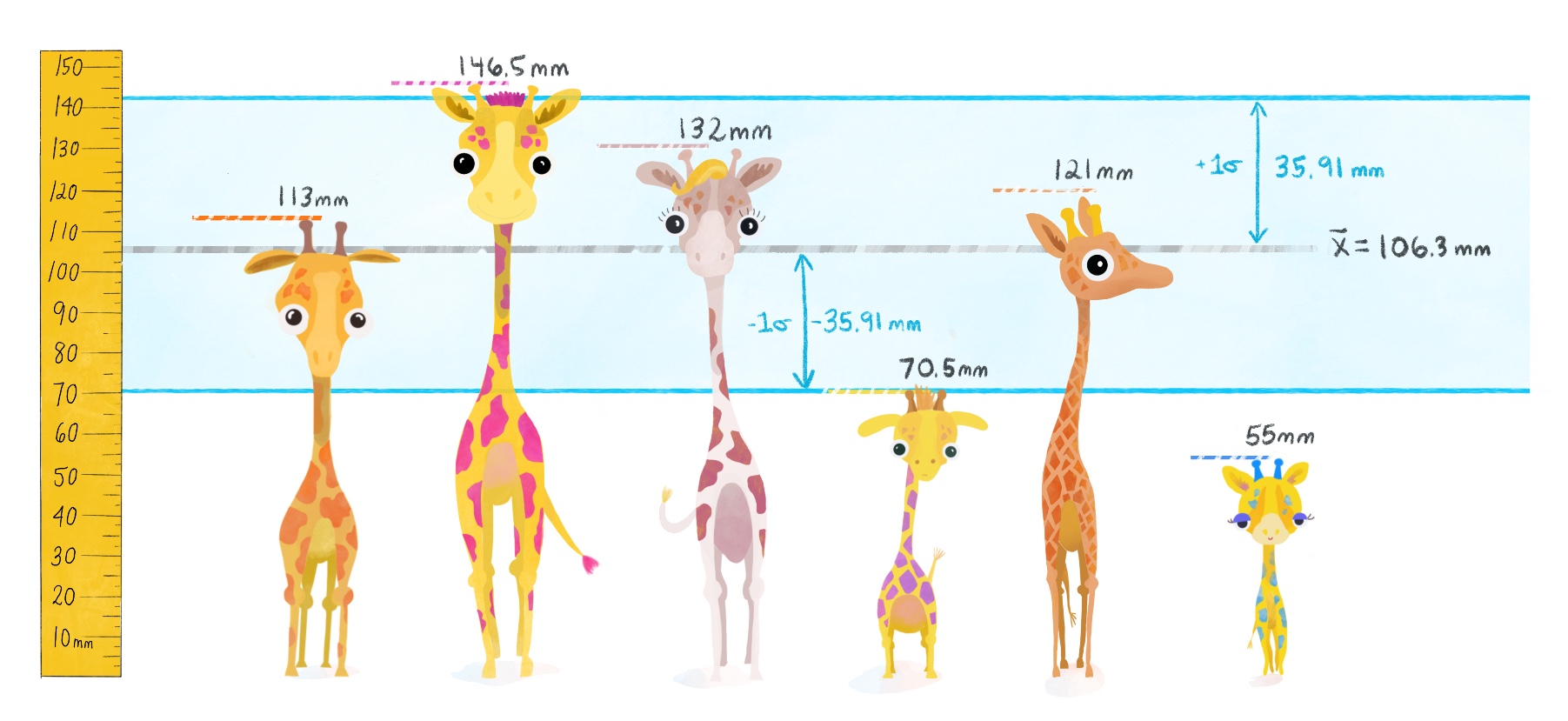
Cuando se habla de desviación estándar, también se puede hacer referencia a la desviación estándar poblacional y la desviación estándar muestral. La desviación estándar poblacional es la desviación estándar de todos los valores en una población completa y se denota con el símbolo \(\sigma\) (sigma). La desviación estándar muestral es la desviación estándar de los valores en una muestra de la población y se denota con el símbolo \(s\). En la práctica, usamos la desviación estándar muestral, ya que rara vez tenemos acceso a todos los datos de una población.

Podemos graficarlo de esta manera, donde se muestra la media y la desviación estándar de las alturas de las jirafas en cada isla como una línea punteada alrededor de la media. Observa cómo la desviación estándar nos da una idea de cuánto varían las alturas alrededor de la media (varían más en la isla 1 que en la isla 2).

Significado de la Desviación Estándar

La desviación estándar nos indica cuánto se desvían los datos de la media.
Puede ser usada para predecir que tan raro o común es un valor en la distribución.
Para una distribución normal, un 97.7% de los datos caen dentro de 3 desviaciones estándar de la media; un 95.4% caen dentro de 2 desviaciones estándar; y un 68.3% caen dentro de 1 desviación estándar.

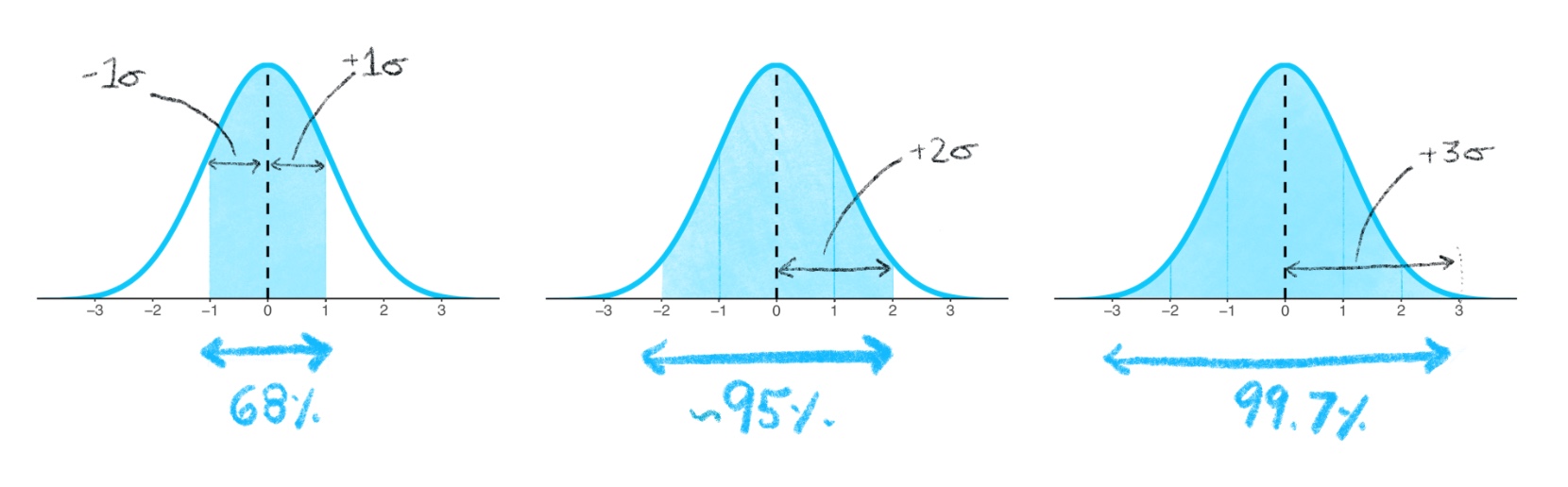
Observa este fenómeno en nustros datos con el siguiente gráfico, donde se muestran las alturas de las jirafas en cada isla y las líneas punteadas representan la media y las líneas de puntos representan 1, 2 y 3 desviaciones estándar de la media. Observa cómo la mayoría de los datos caen dentro de 1, 2 y 3 desviaciones estándar de la media.
Este concepto sera muy importante cuando veamos inferencia estadística ya que nos permitirá hacer predicciones sobre los datos. Por ejemplo, si sabemos que la altura promedio de las jirafas en la isla 1 es de 10 cm con una desviación estándar de 2 cm, podemos predecir que la mayoría de las jirafas tendrán alturas entre 8 y 12 cm (1 desviación estándar), entre 6 y 14 cm (2 desviaciones estándar), y entre 4 y 16 cm (3 desviaciones estándar). Si encontramos una jirafa con una altura de 20 cm, sabemos que es un valor raro, ya que está a más de 5 desviaciones estándar de la media.
Esto es la base de la inferencia estadística, que veremos en futuras lecciones. La inferencia estadística es el proceso de hacer predicciones o sacar conclusiones sobre una población basadas en una muestra de datos.
A partir de la distribución normal, podemos hacer inferencias sobre los datos, es decir, sacar conclusiones sobre la población basadas en nuestra muestra de datos.
Por ejemplo, podemos estimar la probabilidad de que un valor caiga dentro de cierto rango o comparar dos grupos de datos.

Distribución normal estandarizada o Distribución Z

Hasta ahora, hemos visto cómo calcular la media y la desviación estándar de una distribución normal. Sin embargo, en la práctica, a menudo necesitamos comparar diferentes distribuciones normales.
Para facilitar la comparación, podemos estandarizar cualquier distribución normal en una distribución normal estandarizada o distribución Z.
La distribución normal estandarizada es una versión especial de la distribución normal donde la media es 0 y la desviación estándar es 1.

Esto se logra al transformar cualquier distribución normal general en una distribución normal estandarizada mediante la siguiente fórmula:

\[ Z = \frac{X - \mu}{\sigma} \]

Donde:

\(Z\) es el valor estandarizado (con media 0 y desviación estándar 1).
\(X\) es el valor original de la variable.
\(\mu\) es la media de la distribución original.
\(\sigma\) es la desviación estándar de la distribución original.

¿Por qué se hace esto?

La razón por la que se estandarizan las distribuciones es para facilitar la comparación entre diferentes conjuntos de datos. Cuando diferentes distribuciones normales se transforman a una forma común (media = 0 y desviación estándar = 1), es más fácil comparar resultados de diferentes estudios o poblaciones.

Ejemplo

Imagina que estamos trabajando con alturas de personas en un país, donde la media es 170 cm y la desviación estándar es 10 cm.
Si una persona mide 180 cm, podemos estandarizar su altura con la fórmula:

\[ Z = \frac{180 - 170}{10} = 1 \]

Esto significa que esta persona está 1 desviación estándar por encima de la media.
Si otra persona mide 160 cm:

\[ Z = \frac{160 - 170}{10} = -1 \]

Esta persona está 1 desviación estándar por debajo de la media.
Al estandarizar las alturas, podemos comparar fácilmente las alturas de estas dos personas, ya que están en la misma escala de puntuaciones Z.
En R, podemos estandarizar una distribución normal con la función scale(). Observa cómo estandarizamos las alturas de las jirafas en cada isla en el siguiente código.
En este código, hemos estandarizado las alturas de cada jirafa con la función scale(). La función hace lo siguiente: Para cada isla, calculará la media y desviación estándar de las alturas de los individuos. Luego, para cada valor de altura, restará la media de la isla correspondiente y dividirá el resultado por la desviación estándar de esa isla, obteniendo los valores estandarizados.

Ahora, observa qué pasa si calculamos la media y la desviación estándar de las alturas estandarizadas. En una distribución normal estandarizada, la media es 0 y la desviación estándar es 1. Observa cómo se cumple esto en nuestro ejemplo de las alturas de las jirafas. Nota: verás que las medias no son exactamente 0 debido a la precisión de los cálculos en R. Sin embargo, los valores son exponentes muy pequeños, lo que indica que son cercanos a 0.

Ahora, vamos a graficar estas alturas estandarizadas. Observa cómo ahora es más fácil comparar las alturas de las jirafas en cada isla, ya que todas están en la misma escala de puntuaciones Z.
Además, observa cómo la distribución normal estandarizada tiene una media de 0 y una desviación estándar de 1, lo que facilita la comparación entre las alturas de las jirafas en cada isla.
Se resaltan las áreas correspondientes a 1, 2 y 3 desviaciones estándar de la media, que corresponden al 68.27%, 95.45% y 99.73% de los datos en una distribución normal.
No te preocupes por el código. En las próximas lecciones veremos una introducción a la visualización de datos en R. Este es un gráfico un poco más complejo que los que veremos en las primeras lecciones. Sin embargo, más adelante con la práctica, podrás entender y crear gráficos como este en las últimas lecciones del curso.
El gráfico utiliza curvas de densidad, que son estimaciones suavizadas de los histogramas.

Reflexión

Toma en cuenta que en nuestro ejemplo de las jirafas, es probable que no hayamos tomado las alturas de TODAS las jirafas de las islas.
Por lo tanto, nuestro histograma es una aproximación de la verdadera distribución de alturas.
Esta aproximación está basada en nuestro muestreo aleatorio de las alturas. Esto es común en la estadística, donde trabajamos con muestras de datos en lugar de la población completa.
Existe la posibilidad de que nuestro muestreo no sea adecuado para representar la verdadera distribución de alturas en la población. Esto es un tema importante en la estadística y se conoce como error de muestreo.
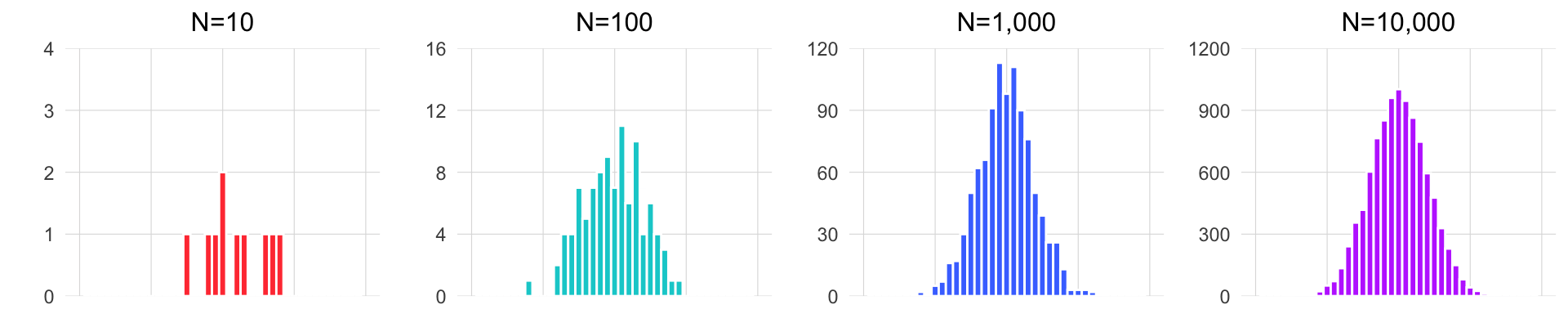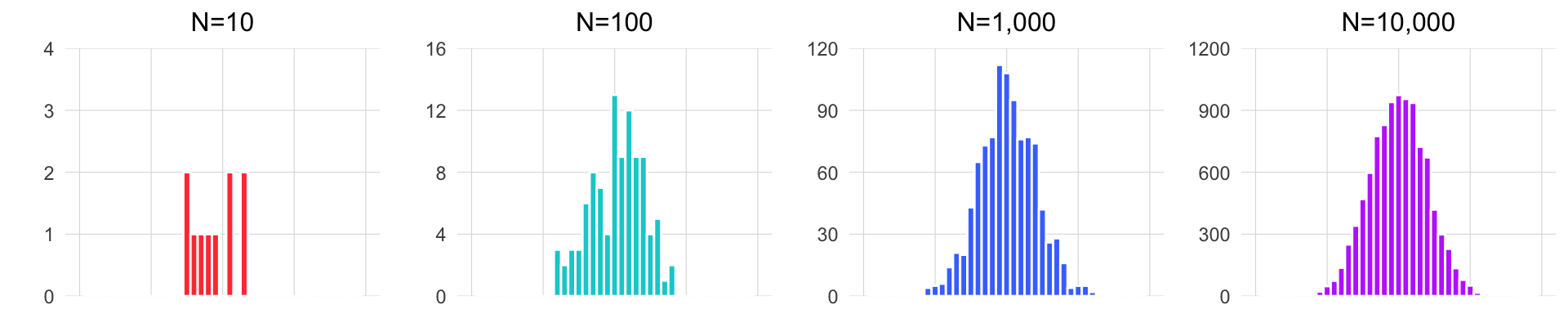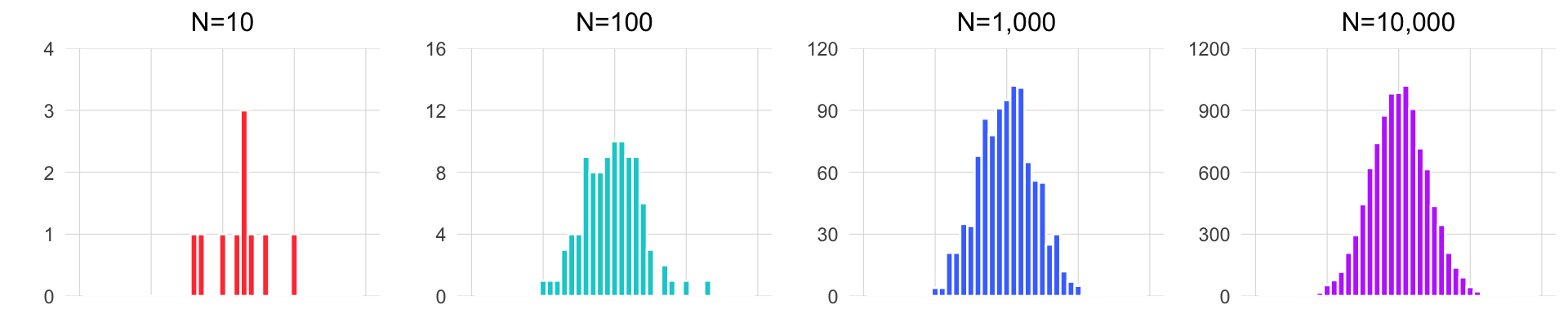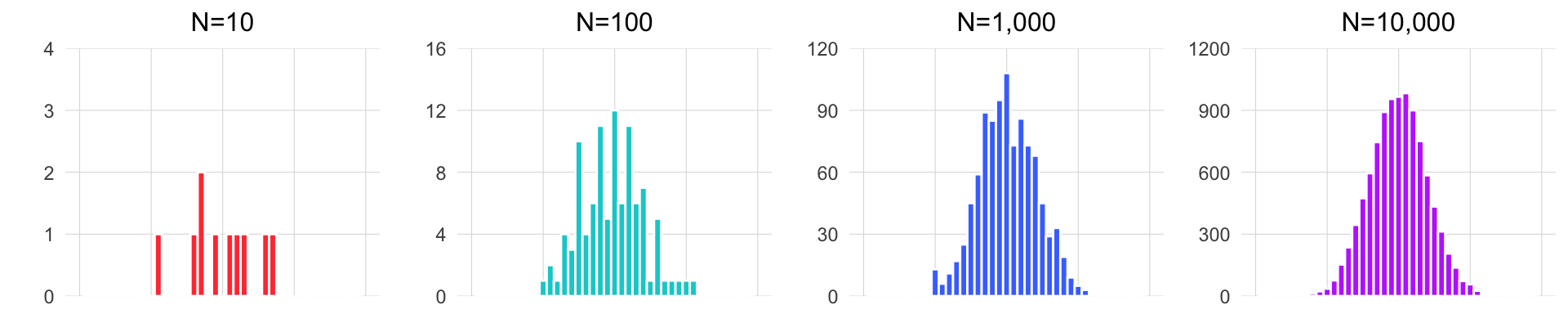
Debido a esto, es importante tomar una muestra lo suficientemente grande y representativa.

Para ilustrar este concepto, observa cómo cambia la forma del histograma al tomar muestras de diferentes tamaños de los datos de las jirafas. El siguiente gráfico muestra el histograma de las jirafas, asumiendo que realizamos un muestreo aleatorio de las alturas varias veces (cada cuadro del GIF representa un muestreo diferente, es decir, cada vez que vamos a la isla y tomamos la altura de N jirafas). En cada muestreo, el número de alturas de jirafas tomadas varía, denotado por la letra N, que indica el tamaño de la muestra. Observa cómo con una muestra pequeña, la forma del histograma cambia drásticamente, mientras que con una muestra grande, se mantiene constante y asemeja la forma de la distribución normal. Esto también se verá más adelante.