Distribuciones de Probabilidad II

Mtro. Santiago Ríos

santiagoboo99@gmail.com

Cursos Orca

Introducción y Objetivos

A pesar de que la distribución normal es la más conocida y utilizada para los datos en biología y medicina, existen muchas otras distribuciones de probabilidad que se pueden aplicar a diferentes tipos de datos.
En esta lección, exploraremos algunas de las distribuciones de probabilidad más comunes y cómo se pueden utilizar en la práctica.
Nuestro objetivo es comprender las características clave de estas distribuciones y cómo se pueden aplicar en el análisis de datos, además de graficarlas en R para visualizar su forma y propiedades.
También aprenderas a simular datos que sigan estas distribuciones con las funciones de R.
Al final de esta lección, tendrás una comprensión más amplia de las distribuciones de probabilidad y cómo se pueden utilizar en tu trabajo de análisis de datos.
Sin embargo, toma en cuenta que en este curso nos centraremos en la distribuciones más comun y útil para la biología y la medicina, la distribución normal.

Distribuciones de Probabilidad

Recordemos que una distribución de probabilidad describe la probabilidad de ocurrencia de cada valor en un conjunto de datos.
Cada distribución tiene sus propias características y propiedades, lo que las hace únicas y útiles para diferentes situaciones.
Algunas de las distribuciones de probabilidad más comunes, sin contar la ya vista dist. normal, incluyen: distribución binomial, distribución de Poisson, distribución exponencial, entre otras.

Distribución Normal

Se caracteriza por su forma de campana y es simétrica alrededor de su media.
La distribución normal tiene dos parámetros clave: la media (\(\mu\)) y la desviación estándar (\(\sigma\)).
En gran parte, los datos en la naturaleza siguen una distribución normal y es fundamental en la teoría detrás de la mayoría de métodos y pruebas estadísticas.
En la siguiente diapositiva generaremos datos simulados que sigan una distribución normal.
Si no te acuerdas de estas funciones, revisa de nuevo la lección anterior de distribuciones de probabilidad y ggplot.

Observa que utilizamos la función rnorm() para generar datos que sigan una distribución normal. Esta función toma tres argumentos principales:
n: número de observaciones aleatorias a ser generadas. En este caso, generaremos 1000 observaciones.
mean: la media de la distribución normal. Establecemos la media en 50.
sd: la desviación estándar de la distribución normal. Establecemos la desviación estándar en 10.
Como estamos generando datos aleatorios, establecemos una semilla (set.seed()) para que los resultados sean reproducibles. Si no estableces una semilla, los resultados serán diferentes cada vez que ejecutes el código (aunque seguirán siendo datos que siguen una distribución normal con media 50 y desviación estándar 10).

Distribución Binomial

La distribución binomial describe el número de éxitos en una secuencia de ensayos independientes (independientes significa que el resultado de un ensayo no afecta el resultado de otro, como lanzar una moneda).
Cada ensayo tiene dos resultados posibles: éxito o fracaso.
Los parámetros clave de la distribución binomial son el número de ensayos (n) y la probabilidad de éxito (p).
Ejemplo de variables con esta distribución: lanzar una moneda o contar el número de éxitos/fracasos en una muestra.
Observa que para simular datos de una distribución binomial, usamos la función rbinom() en lugar de rnorm().
rbinom() genera datos de una distribución binomial con los parámetros especificados. Toma los siguientes argumentos:

rbinom(n,    # Número de observaciones aleatorias a ser generadas
       size, # Número de ensayos (> = 0)
       prob) # La probabilidad de éxito en cada ensayo

Simulemos un experimento donde lanzas una moneda 10 veces y quieres graficar un histograma que represente el número de caras obtenidas. Repetirás este experimento por 100 días. Como solo hay dos resultados posibles, cara o cruz, nuestra probabilidad de éxito es 0.5 o 50%. La función rbinom() tiene tres argumentos principales:

n: número de experimentos (en este caso, cuántas veces repetimos el experimento de lanzar la moneda 10 veces). Supongamos que repetimos el experimento 100 veces.
size: número de lanzamientos por experimento (en este caso, 10 lanzamientos por experimento).
prob: probabilidad de éxito (en este caso, la probabilidad de obtener cara, que es 0.5 para una moneda justa).

El histograma mostrará la distribución del número de caras obtenidas en 10 lanzamientos de moneda, repetidos 100 veces.
Dado que las probabilidades son simétricas (0.5 para cara y 0.5 para cruz), la distribución tendrá una media en torno a 5 (la mitad de los lanzamientos deberían ser caras, en promedio), pero con variabilidad en los resultados.
Los valores extremos (muy pocos o muchas caras) serán menos frecuentes.
Ahora imagina que repetimos el experimento, pero con una moneda cargada que tiene una probabilidad de 0.85 de obtener cara. ¿Cómo crees que cambiaría la distribución de los resultados? Antes de correr el código, piensa en cómo se vería el histograma.

Distribución de Poisson

La distribución de Poisson es una distribución de probabilidad que describe el número de eventos que ocurren en un intervalo de tiempo o espacio, cuando estos eventos suceden de manera independiente y con una tasa promedio constante.
Se utiliza para modelar eventos raros o inusuales, como accidentes, llamadas telefónicas, o errores en un proceso.
La distribución de Poisson tiene un solo parámetro, la tasa de ocurrencia (\(\lambda\)), que representa el número promedio de eventos en el intervalo.
La distribución de Poisson es útil para modelar eventos discretos y se utiliza en situaciones donde los eventos son raros y aleatorios.
A continuación, veremos cómo se ve la distribución de Poisson y cómo se puede aplicar en la práctica.

Un ejemplo de una variable con esta distribución es el número de mutaciones en una cadena de DNA en una determinada región durante un período de tiempo fijo.
Imagina que estamos investigando el número de mutaciones en una sección de ADN en células cancerígenas.
Sabemos, a partir de estudios previos, que en promedio ocurren 3 mutaciones por célula. Queremos simular y visualizar la distribución de mutaciones en 1000 células.

En este caso, la tasa promedio de mutaciones por célula es 3 y el suceso que estamos modelando es el número de mutaciones en una célula. Usaremos la función rpois() para simular datos que sigan una distribución de Poisson. Esta función toma dos argumentos principales: - n: número de observaciones aleatorias a ser generadas. - lambda: la tasa de ocurrencia de eventos en un intervalo de tiempo o espacio. - En este caso, generaremos 1000 observaciones de la distribución de Poisson con una tasa de ocurrencia de 3 mutaciones por célula.

El histograma muestra la distribución del número de mutaciones por célula en 1000 células. Dado que usamos una distribución de Poisson con un parámetro \(\lambda\) = 3, esperamos que:
El pico del histograma esté alrededor de 3 (el número promedio de mutaciones por célula).
La distribución será asimétrica, con más células concentradas en el rango de mutaciones bajas, y una “cola” que se extiende hacia la derecha a medida que aumentan el número de mutaciones.
Puedes ajustar el número de células para cambiar el tamaño de la muestra o cambiar el valor de lambda para simular una tasa diferente de mutaciones por célula.

Otras Distribuciones

Además de la distribución normal, binomial y de Poisson, existen muchas otras distribuciones de probabilidad que se utilizan en diferentes contextos.
En este enlace y este puedes encontrar una lista de las distribuciones de probabilidad que puedes encontrar en R.
Aunque en el curso nos enfocaremos en la distribución normal, veremos que muchas pruebas estadísticas utilizan otras distribuciones, por lo que es útil conocerlas y comprender sus propiedades.
Algunos de estos ejemplos, son la distribución chi-cuadrada, t de Student, F de Fisher, entre otras que son fundamentales en la inferencia estadística y en el análisis de datos.
Solo para conocerlas, veamos rápidamente algunas de estas distribuciones utilizadas en análisis estadístico.

Distribuciones y pruebas asociadas

Distribución	Prueba estadística asociada	Aplicaciones en Biomedicina
t de Student	Prueba t (una muestra, dos muestras independientes, pareada)	Comparación de medias de biomarcadores, tratamientos, etc.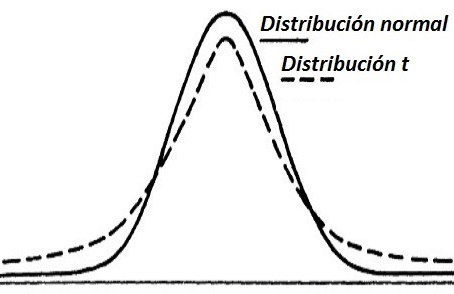
Chi-cuadrada (χ²)	Prueba de bondad de ajuste, prueba de independencia (χ²)	Comparación de frecuencias, análisis de tablas de contingencia
F de Fisher	ANOVA, pruebas de igualdad de varianzas, regresión	Comparación de varios tratamientos, análisis de regresión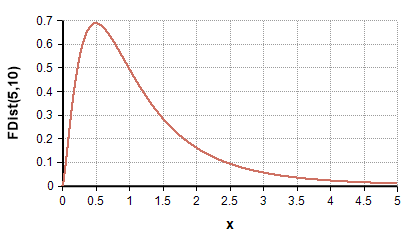
Normal (Z)	Prueba Z, intervalos de confianza	Comparación de medias para grandes muestras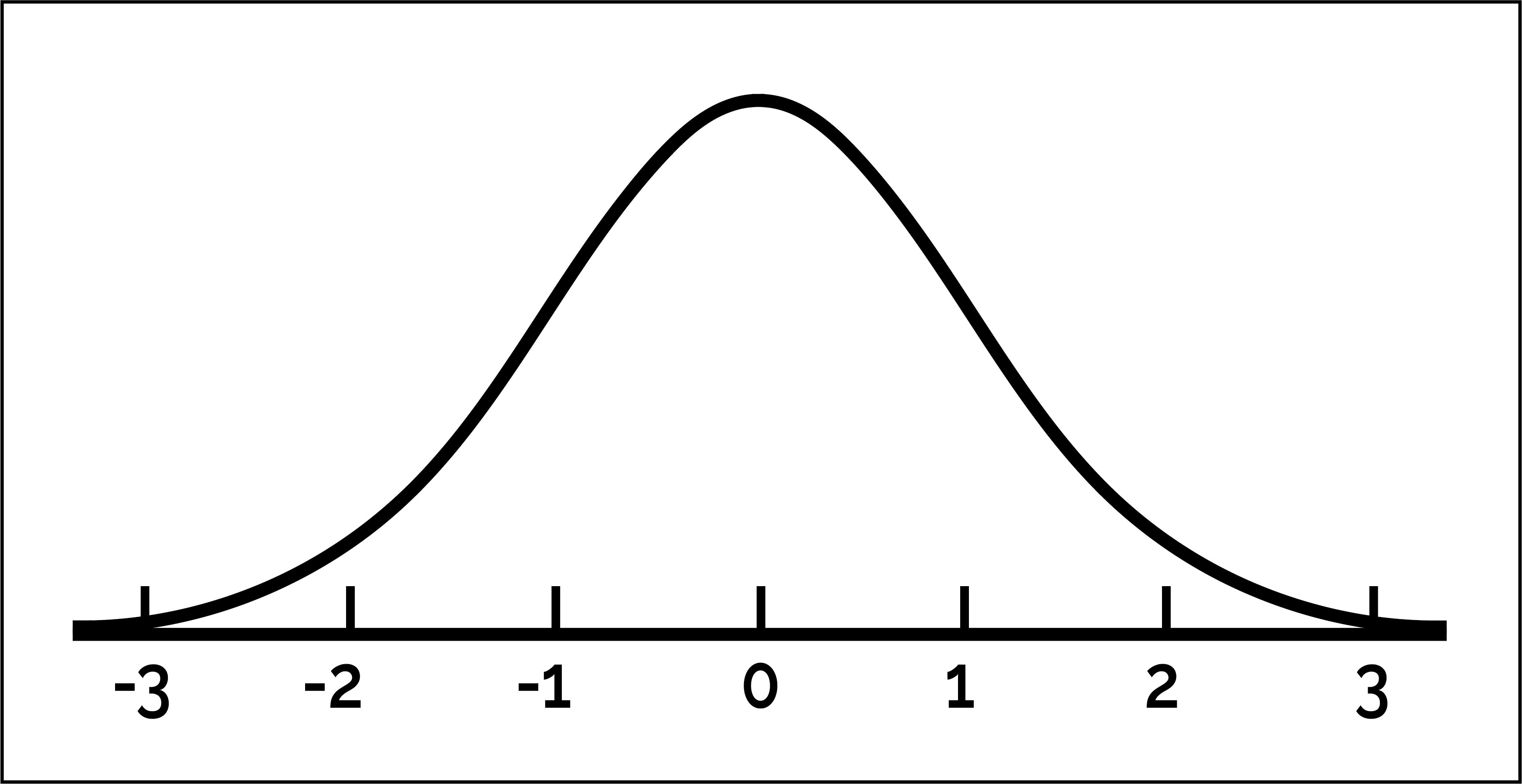
Binomial	Prueba binomial, prueba exacta de Fisher	Evaluación de proporciones de éxito (por ejemplo, respuesta a un tratamiento)